Информационно-коммуникационные технологии
в педагогическом образовании

ИСПОЛЬЗОВАНИЕ МЕТОДА ЗАМЕНЫ ПЕРЕМЕННОЙ ПРИ РЕШЕНИИ УРАВНЕНИЙ С ПАРАМЕТРАМИ В ЕГЭ ПО МАТЕМАТИКЕ

Раздел: Проблемы и перспективы современного физико-математического образования

Журнал: Материалы VI Международной очно-заочной научно-практической конференции «Проблемы и перспективы современного образования: практика вуза и школы», Ч. 1

27 февраля 2022 г.

Авторы: Гридчина Валентина Борисовна

Информационно-коммуникационные технологии в педагогическом образовании. http://infed.ru

_______________________________________________________________________

УДК 372. 851

В. Б. Гридчина

V. B. Gridchina

Гридчина Валентина Борисовна, к. п. н., доцент, КГПИ КемГУ, г. Новокузнецк, Россия.

Gridchina Valentina Borisovna, candidate of pedagogical Sciences, associate Professor, Kuzbass Humanitarian Pedagogical Institute of Kemerovo State University, Novokuznetsk, Russia.

 

ИСПОЛЬЗОВАНИЕ МЕТОДА ЗАМЕНЫ ПЕРЕМЕННОЙ ПРИ РЕШЕНИИ УРАВНЕНИЙ С ПАРАМЕТРАМИ В ЕГЭ ПО МАТЕМАТИКЕ

USING THE METHOD OF REPLACEMENT OF A VARIABLE IN SOLVING EQUATIONS WITH PARAMETERS IN THE USE IN MATHEMATICS

 

Аннотация. В статье рассмотрены методические рекомендации для обучения школьников решению уравнений с параметрами с использованием метода замены переменной. Автор выделяет затруднения, с которыми сталкиваются учащиеся, решая подобные задачи на ЕГЭ по математике и показывает пути их преодоления.

Annotation. The article discusses methodological recommendations for teaching schoolchildren to solve equations with parameters using the change of variable method. The author highlights the difficulties that students face when solving similar problems at the USE in mathematics and shows ways to overcome them.

Ключевые слова: задачи с параметрами, уравнения с параметрами, замена переменной, ЕГЭ по математике.

Keywords: tasks with parameters, equations with parameters, change of variable, USE in mathematics.

 

Согласно аналитическим данным Федерального института педагогических измерений в 2019-2021 годах с задачей с параметром (уравнения и неравенства с параметрами) справились в среднем 2,9 % сдававших ЕГЭ по математике, что свидетельствует о низком уровне готовности учащихся к решению подобного типа заданий [1-3].

Такая ситуация объясняется тем, что, как правило, не существует единого алгоритма их решения, каждая задача с параметрами требует от учащихся индивидуального нестандартного подхода. Для решения таких задач учащимся необходима хорошая математическая подготовка, а также умения: на основе проведенного анализа условий осуществлять поиск решения; находить различные варианты решения, анализировать полученные результаты.

Очень часто при введении новой переменной в ходе решения задач с параметрами получается квадратное уравнение. Для случая, когда новая переменная сравнивается с нулем, удобно использовать специальную аналитическую таблицу. С ее помощью задача с параметром сводится к стандартным ситуациям, в которых анализируются условия: квадратное уравнение имеет два различных положительных корня; два различных отрицательных корня; корни разных знаков и т.д.

Рассмотрим несколько примеров, демонстрирующих использование такой таблицы.

Пример 1. При каких значениях параметра α уравнение  имеет ровно один корень?

Решение. Сделаем замену:  = t, t > 0.

Получим квадратное уравнение с параметром t² - 2αt + 3 - α = 0. Здесь учащиеся очень часто рассуждают следующим образом: квадратное уравнение имеет один корень, когда дискриминант равен нулю. При этом они не указывают, что этот корень должен быть положительным, а также забывают рассмотреть другие случаи: корни уравнения имеют разные знаки; один из корней положителен, другой равен нулю. Чтобы учесть все возможные случаи, мы предлагаем заполнить аналитическую таблицу, в которой укажем знаки корней квадратного уравнения и соответствующее количество корней исходного уравнения.

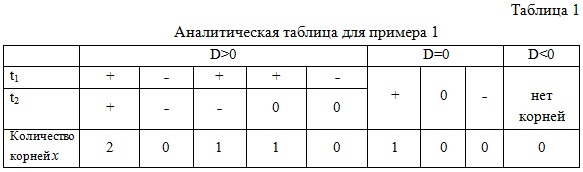
Из таблицы 1 можно увидеть, какие случаи нужно рассмотреть, чтобы исходное уравнение имело ровно один корень.

Запишем теорему Виета для данного квадратного уравнения:

Найдем дискриминант: D = (-2α)² - 4(3 - α) = 4(α² + α - 3).

Рассмотрим три возможных случая.

Случай 1. Квадратное уравнение имеет корни разных знаков.  

Случай 2. Один из корней положителен, другой равен нулю.

Случай 3. Дискриминант равен нулю, уравнение имеет один положительный корень.

Дискриминант равен нулю, если , при этом уравнение имеет один корень t = α.

При α =   t < 0, при α =    t > 0. Условию задачи удовлетворяет α =  .

После объединения всех случаев, запишем ответ: α  [3; ∞ ); .

Пример 2. При каких значениях параметра α уравнение x² - (α + 1)·|x| + 3 - 2α² = 0 имеет четыре корня?

Решение. Сделаем замену: |x| = t, t ≥ 0.

Учитывая тождество |x|² = x² , получим квадратное уравнение с параметром t² - (α + 1)·t + 3 - 2α² = 0 . Составим аналитическую таблицу, в которой укажем знаки корней квадратного уравнения и соответствующее количество корней исходного уравнения.

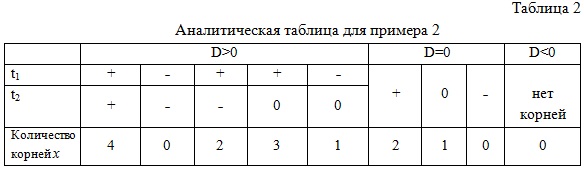
Из таблицы 2 видно, что для того, чтобы исходное уравнение имело четыре различных корня квадратное уравнение должно иметь два различных положительных корня.

Запишем теорему Виета для данного квадратного уравнения:

Найдем дискриминант: D = (α + 1)² - 4(3 - 2α²) = 9α² + 2α - 11.

Запишем достаточные условия для того, чтобы квадратное уравнение имело два различных положительных корня: дискриминант больше нуля, произведение и сумма корней больше нуля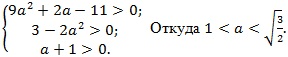   

Ответ:

Данный подход также можно использовать для решения биквадратных уравнений с параметрами.

Пример 3. Найти все значения параметра α, при которых уравнение  не имеет корней?

Сделаем замену: x² = t, t ≥ 0. Получим уравнение t² - (α + 2)t + 1 - α = 0.

Решая данное уравнение, многие учащиеся приводят следующие рассуждения: квадратное уравнение не имеет корней, если дискриминант меньше нуля. Про остальные случаи они забывают.

Запишем теорему Виета для данного квадратного уравнения:

Найдем дискриминант D = α² + 8α.

В данной задаче также можно использовать Таблицу 2. В соответствии с таблицей, для того, чтобы исходное уравнение не имело корней, нужно рассмотреть три случая:

Случай 1. Квадратное уравнение имеет два различных отрицательных корня.

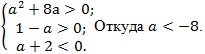
Случай 2. Дискриминант равен нулю и уравнение имеет один отрицательный корень.

Дискриминант равен нулю, если α = -8 или α = 0 , при этом уравнение имеет один корень   Но только α = -8  удовлетворяет условию задачи.

Случай 3. Дискриминант меньше нуля.

α² + 8α < 0. Решая это неравенство, получим: -8 < α < 0.

После объединения всех случаев, запишем ответ: α  (-∞; 0).

Описанный подход к решению уравнений с параметрами учащиеся могут использовать на итоговой аттестации. Аналитическая таблица, составленная для конкретного уравнения, позволит учащимся увидеть зависимость числа корней исходного уравнения (показательного, биквадратного, с модулем и др.) от знака корней квадратного уравнения и без труда описать каждый полученный случай.

Список литературы

1. Ященко, И. В. Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2019 года по МАТЕМАТИКЕ [Электронный ресурс]. / И. В. Ященко, И. Р. Высоцкий, А. В. Семенов – М., 2019. – 25 с. – URL : http://fipi.ru/sites/default/
   files/document/1567500409/matematika_2019.pdf (дата обращения : 07.02.2022).
2. Ященко, И. В. Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2020 года по МАТЕМАТИКЕ [Электронный ресурс]. / И. В. Ященко, И. Р. Высоцкий, А. В. Семенов – М., 2020. – 17 с. – URL : https://doc.fipi.ru/ege/analiticheskie-i-metodicheskie-materialy/2020/Matematika_mr_2020.pdf (дата обращения : 07.02.2022).
3. Ященко, И. В. Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2021 года по МАТЕМАТИКЕ [Электронный ресурс]. / И. В. Ященко, И. Р. Высоцкий, А. В. Семенов – М., 2021. – 31 с. – URL : https://doc.fipi.ru/ege/analiticheskie-i-metodicheskie-materialy/2021/ma-mr-2021.pdf (дата обращения : 07.02.2022).