Информационно-коммуникационные технологии
в педагогическом образовании

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ В РЕШЕНИИ ПРОФЕССИОНАЛЬНЫХ ЗАДАЧ

Раздел: Материалы II Международной очно-заочной научно-практической конференции «Проблемы и перспективы современного физико-математического, информационного и технологического образования» (Новокузнецк, февраль 2018)

Журнал: Проблемы и перспективы современного физико-математического образования

27 февраля 2018 г.

Авторы: Падалка Венера Нагимовна , Шац Татьяна Владимировна

УДК [517.2:622.2]:004.4

В. Н. Падалка, Т. В. Шац

V. N. Padalka, T. V. Shats

Падалка Венера Нагимовна, преподаватель иностранного языка, ГПОУ ОГТК, г. Осинники.

Шац Татьяна Владимировна, преподаватель математики, ГПОУ ОГТК, г. Осинники.

Padalka Venera Nagimovna, foreign languages teacher, GPOU OGTK, Osinniki.

Shats Tatyana Vladimirovna, mathematics teacher, GPOU OGTK, Osinniki.

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ В РЕШЕНИИ ПРОФЕССИОНАЛЬНЫХ ЗАДАЧ

DIFFERENTIAL CALCULUS IN THE SOLUTION OF PROFESSIONAL TASKS

Аннотация. Статья посвящена проблеме формирования устойчивого интереса к изучению математики как средства решения профессиональных задач. Приводится расчет оптимальных размеров сечений горных выработок, проведенный методами дифференциального исчисления (рисунки к задачам выполнены в программе AutoCAD), расчет параметров сечений в программе Microsoft Office Excel 2007, сопоставление полученных данных с табличными.

Annotation. The article is devoted to the problem of forming a steady interest in the study of mathematics as a mean of solving professional tasks. The calculation of the optimal sizes of sections of mine workings, carried out by methods of differential calculus (drawings to tasks are done in the program AutoCAD), calculation of section parameters in the program Microsoft Office Excel 2007, comparison of the received data with tabular ones.

Ключевые слова: оптимальные размеры сечений горных выработок, методы дифференциального исчисления, расчет параметров, типовые сечения.

Keywords: optimal sizes of sections of mine workings, methods of differential calculus, calculation of parameters, typical sections.

 

Большую часть своих усилий человек тратит на поиск наилучшего, или как часто говорят, оптимального, решения поставленной задачи. Как, располагая определёнными ресурсами, добиться наиболее высокого жизненного уровня, наивысшей производительности труда, наименьших потерь, максимальной прибыли, минимальной затраты времени – так ставятся вопросы, над которыми приходится думать каждому члену общества. Не все такие задачи поддаются точному математическому описанию, не для всех из них найдены короткие пути решения. Однако часть таких задач поддаётся исследованию с помощью методов математического анализа – это задачи, которые можно свести к нахождению наибольшего и наименьшего значения функции.

По мере развития горной техники и технологии, задачи, связанные с расчетами оптимальных размеров сечений горных выработок, решались теоретически или экспериментально и результаты в виде методик и таблиц вводились в справочные издания. При работе со справочником специалисту достаточно произвести необходимые алгебраические расчеты или выбрать параметры по таблицам [3].

Форма поперечного сечения выработки определяется удобством ее эксплуатации, условиями сохранения длительной ее устойчивости, материалом и конструкцией крепи и другими факторами.

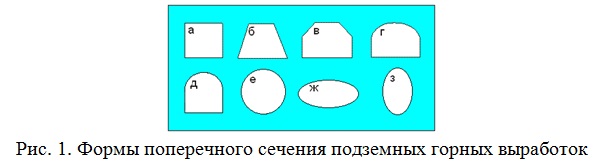
Прямоугольная форма (рис. 1, а) чаще всего используется при отсутствии бокового давления пород и в тех случаях, когда выработки крепятся деревянной, штанговой (анкерной) или смешанной крепью (бетонные стенки и перекрытия из металлических балок). Трапециевидное сечение воспринимается как вертикальное, при этой форме выработки обычно крепят деревом, металлом, сборным железобетоном (рис. 1, б). Полигональная форма принимается в том случае, когда выработки крепят железобетоном, реже – для усиления трапециевидной деревянной крепи (рис. 1, в). Сводчатую форму применяют при каменной или бетонной крепи. При этом свод бывает трехцентовый (коробовой) и полуциркульный с прямолинейными или криволинейными стенами (рис. 1, г). Арочное сечение используется при наличии вертикального и бокового давления горных пород (рис. 1, д). Обычно выработки крепятся металлическими арками разных конструкций [6].

Размеры выработок принимают в соответствии с типовыми сечениями, т. к. сечения выработок стандартизованы. Площадь поперечного сечения стволов изменяется от 12 до 60 м, что для круглого сечения соответствует диаметру ствола от 4 до 9 м.

Крепь горных выработок должна удовлетворять следующим основным техническим и экономическим требованиям:

• быть прочна, устойчива, долговечна и обеспечивать рабочее состояние выработок и безопасные условия труда в течение всего срока службы;
• иметь минимальные затраты на изготовление, доставку, возведение и эксплуатацию;
• не препятствовать выполнению производственных процессов при проведении выработок и её эксплуатации;
• занимать в выработке минимальную площадь в поперечном сечении;
• иметь минимальный коэффициент аэродинамического сопротивления [5].

Расчет оптимальных размеров сечений горных выработок (арочная, штанговая и трапециевидная).

Задача 1.

Поперечное сечение горной выработки, закрепленной арочной стальной крепью, имеет форму прямоугольника, завершенного полукругом (рис. 2, 3). Площадь поперечного сечения выработки (например, коренного штрека) равна S=7,6 м. При каком радиусе полукруга периметр сечения выработки является наименьшим? [2]

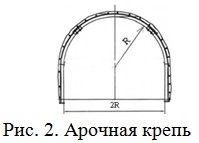
Определим периметр выработки: L = 2h + 2R + πR.

Площадь поперечного сечения выработки составляет:  выразим

Подставляя выражение для h в формулу периметра получим:

, следовательно имеем .

Найдем производную функции 

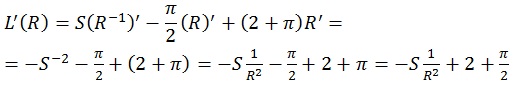
Определим критические точки 

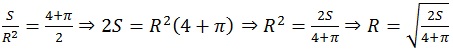
 Найдем вторую производную

 

L''(R)>0, следовательно функция L(R) в точке имеет наименьшее значение. Для S=7,6 м найдем 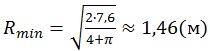 [1].

 

Выполним в программе Microsoft Office Excel 2007 нахождение параметра R сечения горной выработки в зависимости от изменения площади сечения S по формуле 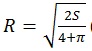 (рис. 4).

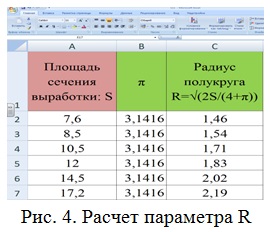
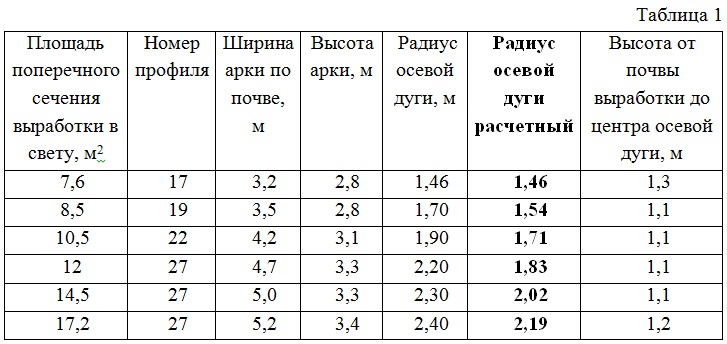
Сравним полученные значения радиуса сечения выработки с таблицей 1 [3].

Задача 2.

Сечение горной выработки, закрепленной штанговой крепью (рис. 5), на прямолинейном участке обычно имеет прямоугольную форму (например, просек или печь). Площадь поперечного сечения выработки S = 4,7 м. Определить наименьший периметр крепежной рамы.

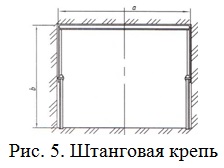
Периметр L крепежной рамы составляет: L = a + 2b. Так как S = ab, то a = S/b. Отсюда найдем  Исследуем функцию L(b) на экстремум [1].

Найдем первую производную 

Решая уравнение 

Так как , то функция L(b) в точке b=bкр имеет минимум. Таким образом,

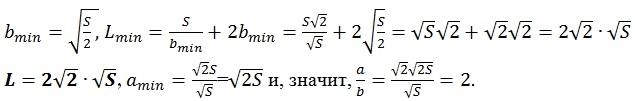
В данном случае .

В справочнике [4] приведено значение .

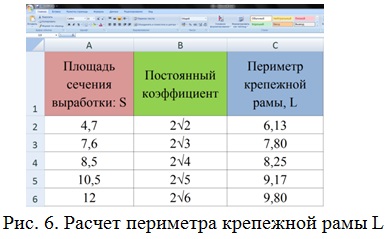
Выполним нахождение периметра крепежной рамы L в зависимости от изменения площади сечения S по формуле (рис. 6).

Математические методы занимают ведущее место в горноэкономическом анализе. Мы рассмотрели лишь один аспект применения этих методов, с целью показать студентам горных специальностей необходимость овладения математическими методами исследования функции для использования в профессиональной деятельности.

Список литературы

1. Богомолов, Н. В. Практические занятия по математике [Текст]: учеб. пособие для средних спец. учеб. заведений / Н. В. Богомолов. – 6-е изд., стер. – Москва : Высш. шк., 2003. – 495 с.
2. Райхмист, Р. Б. Математика в горном деле: задачи и упражнения [Текст]: учеб. пособие для средних спец. учеб. зав. / Р. Б. Райхмист, Л. В. Ершов. – Москва: Высш. шк., 1998. – 79 с.
3. Сборник типовых сечений горных выработок [Текст]. – М.: «Недра», 1985.
4. Шехурдин, В. К. Задачник по горным работам, проведению и креплению горных выработок [Текст]: учеб. пособие для средних спец. учеб. заведений / В. К. Шехурдин. – М.: «Недра», 1995. – 239 с.
5. Горнопромышленный Портал России: все о горной промышленности [Электронный ресурс] // Режим доступа: http://www.miningexpo.ru/. (дата обращения 16.01.2018)
6. Горные выработки и их классификация [Электронный ресурс] // Режим доступа: https://infopedia.su/3x22d2.html. (дата обращения 18.01.2018).