ФОРМИРОВАНИЕ НАУЧНЫХ МЕТОДОВ ПОЗНАНИЯ ПРИ ОБУЧЕНИИ ПЛАНИМЕТРИИ В УСЛОВИЯХ РЕАЛИЗАЦИИ ФГОС
Раздел: Современные педагогические технологии организации урочной и внеурочной деятельности в условиях реализации ФГОС
Журнал: Материалы III Международной очно-заочной научно-практической конференции. Часть 3
8 мая 2019 г.
Авторы: Шагиева Юлия Вячеславовна
УДК 373.5.016:514
Ю. В. Шагиева
Y. V. Shagieva
Шагиева Юлия Вячеславовна, учитель математики, МБОУ «Лицей № 35», г. Нижнекамск.
Shagieva Yuliya Vyacheslavovna, mathematics teacher, «Lyceum № 35», Nizhnekamsk.
ФОРМИРОВАНИЕ НАУЧНЫХ МЕТОДОВ ПОЗНАНИЯ ПРИ ОБУЧЕНИИ ПЛАНИМЕТРИИ В УСЛОВИЯХ РЕАЛИЗАЦИИ ФГОС
FORMATION OF THE HUMAN RESOURCES METHODS IN TEACHING PLANIMETRY IN THE CONDITIONS OF GEF IMPLEMENTATION
Аннотация. В работе рассматриваются способы формирования научных методов познания при изучении геометрии в условиях реализации ФГОС.
Annotation. The paper discusses the ways of forming scientific methods of knowledge in the study of geometry in the conditions of implementation of the federal state educational standard.
Ключевые слова: научные методы познания, универсальные учебные действия, метапредметные знания.
Keywords: scientific methods of cognition, universal learning activities, meta-subject knowledge.
Федеральные государственные образовательные стандарты (ФГОС) перед школьным образованием поставили новые задачи. Одна из задач: обеспечение единства образовательного пространства Российской Федерации, единых требований по формированию универсальных учебных действий (УУД). Универсальные учебные действия, по сути, являются конкретизированными целями образования.
На текущем этапе реформирования образования выдвигаются требования к формированию у обучающихся метапредметных знаний, умений и навыков. Реализация данных требований должна выполняться на уроках геометрии через формирование научных методов познания.
В процессе обучения геометрии основной школы традиционный подход приводит к понижению интереса у обучающихся к этому предмету, особенно среди тех учеников, кому трудно даётся предмет математика. Основная причина этого состоит в том, что формулировки и доказательства теорем обучающиеся учат наизусть, без осмысления материала, а доказательства не проверяются, не анализируются. Данный подход к обучению приводит к развитию у обучающихся стандартного мышления, что является одной из причин отвержения данного стиля современными школьниками. Эту проблему поможет решить применение математического пакета в разных видах учебной деятельности [3].
Программа «Живая Математика» легко осваивается, для помощи в ознакомлении и применении имеется руководство в методических материалах программы. Данную программу можно использовать не только на уроках, но и во внеурочной деятельности, при самостоятельном обучении, индивидуальных занятиях [4].
Приведенные ниже примеры 1-3 позволяют, используя программу «Живая математика», организовывать самостоятельный вывод свойств, теорем, доказательства обучающимися, так как в программе удобно применять такие научные методы познания, как моделирование, наблюдение и эксперимент.
Пример 1. При изучении темы «Параллелограмм» в 8 классе изучается свойство: «В параллелограмме противоположные стороны равны и противоположные углы равны» [1].
Подвести учеников к этому свойству можно следующим образом:
- Постройте параллелограмм (построить два отрезка с общей точкой, построить параллельную прямую каждому отрезку, поставить точку на пересечение параллельных прямых, скрыть параллельные прямые, соединить точку с исходными отрезками).
- Выделить две противоположные стороны, во вкладке «Измерения» выберите команду «Длина». На экране появятся измерения длин противоположных сторон.
- Поэкспериментируйте, выделите вершину параллелограмма, перемещайте её и наблюдайте за результатами вычисления. Сделайте вывод.
- Измерьте противоположные углы, для этого выделите точки, образующие угол, во вкладке «Измерения» выберите команду «Угол», так же и с другим углом.
- Поэкспериментируйте, выделите вершину параллелограмма, перемещайте её и наблюдайте за результатами вычисления углов. Сделайте вывод.
- Запишите то, что у вас получилось. В параллелограмме противоположные стороны равны и противоположные углы равны.
Таким образом, обучающиеся сами выведут свойство, через моделирование, наблюдение, эксперимент (рис. 1). Примечание: для построения параллельной прямой, нужно выделить прямую, относительно которой нужно провести параллельную, и точку, через которую будет проходить параллельная прямая; выбрать во вкладке меню «Построение», команда «Параллельная прямая».
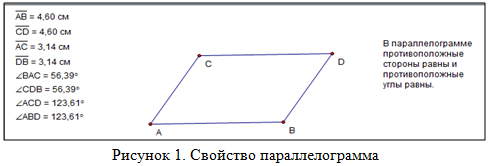
Формировать научные методы познания, применяя математический пакет «Живая Математика», можно не только при выводе свойств, теорем, но и при выполнении построений для решения задач.
Пример 2
Задание:
- Начертите выпуклые пятиугольник и шестиугольник. В каждом многоугольнике из одной вершины проведите все диагонали.
- Посчитайте, на сколько треугольников делится каждый многоугольник.
- Учитывая сумму углов треугольника и количество треугольников, выведите формулу нахождения суммы углов выпуклого многоугольника.
- Проверьте правильность формулы с помощью команды «Угол» во вкладке «Измерения».
- Сделайте вывод, запишите формулу (рис. 2).
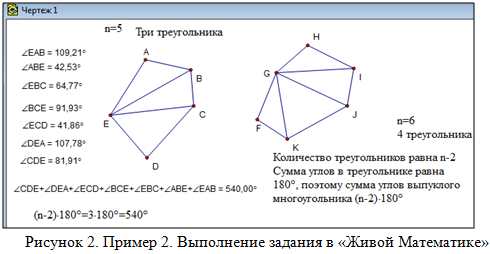
Примечание: Чтобы найти сумму вычислений, нужно во вкладке «Измерения» выбрать команду «Вычислить…». Далее в появившемся окне ввести формулу и нажать готово.
Пример 3. Задача: «Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр этого параллелограмма, если BK=15 см, KC= 9 см» [2].
1. Постройте изображение к задаче.
Чтобы построить биссектрису нужно выполнить следующие действия: выделите точки, образующие угол A, Во вкладке выберите «Построение» команду «Биссектриса». Отметьте точку пересечения биссектрисы и прямой ВС, постройте отрезок AK. Решите задачу (рис. 3). Примечание: если биссектриса угла не пересекаете отрезок ВС, то измените параллелограмм, переместив за вершину.
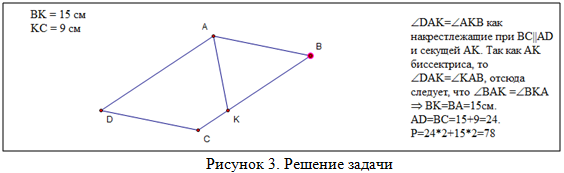
Таким образом, обучающиеся, при работе с программой, научатся самостоятельно выводить свойства, доказывать и применять теоремы, тем самым они будут осмысленно изучать материал, а не учить его наизусть. Через формирование научных методов познания, применяя новые технологии, можно повысить не только интерес к изучаемому предмету, но и качество обучения.
Список литературы
- Вернер, А. Л. Геометрия : Учеб. пособие для 8 кл. общеобразоват. учреждений [Текст]. / А. Л. Вернер, В. И. Рыжик, Т. Г. Ходот. – М. : Просвещение, 2001. – 192 с.
- Атанасян, Л. С. Геометрия. 7-9 классы: учеб. для общеобразоват. учреждений [Текст]. / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – 20-е изд. – М. : Просвещение, 2010. – 384 с.
- Далингер, В. А. Методика обучения учащихся доказательству математических предложений: кн. для учителя [Текст]. / В. А. Далингер. – М. : Просвещение, 2006. – 256 с.
- Учебно-методический комплект «Живая Математика».
