СМЕШАННАЯ КРАЕВАЯ ЗАДАЧА ДЛЯ ОБОБЩЕННОГО УРАВНЕНИЯ БУССИНЕСКА
Раздел: Научно-практическая работа студентов педагогического вуза
Журнал: Научно-практическая деятельность студентов педагогического вуза
13 июня 2012 г.
Авторы: Маланьина И. Г.
И. Г. Маланьина
Научный руководитель: Фураев Валерий Зиновьевич.
СМЕШАННАЯ КРАЕВАЯ ЗАДАЧА ДЛЯ ОБОБЩЕННОГО УРАВНЕНИЯ БУССИНЕСКА
Рассмотрим начально-краевую задачу для уравнения
с неоднородными граничными условиями
где 
и начальным условием
(3)
Введем функцию
И записываем уравнение (1) в виде
(4)
Вводя функцию Грина 
для оператора 
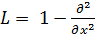с нулевыми условиями на концах отрезка [0,1], из (4) получим:
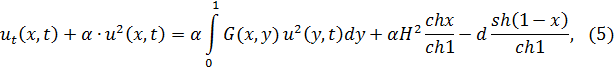
где
Если начальная функция 
непрерывна и неотрицательна на отрезке [0,1] то задача (5), (3) однозначно разрешима в целом, т. е. на отрезке [0,T] для любого T>0 [1. С. 2014 - 2015].
Таким образом, данная смешанная начально-краевая задача сводится к задаче Коши для интегро-дифференциального уравнения (5) с начальным условием (3).
Решение данной задачи может быть найдено методом Эйлера, по формуле:
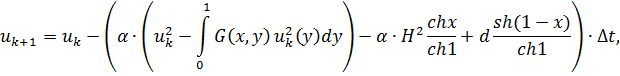
где 
Для численного решения задачи интеграл в правой части по пространственной переменной y вычисляется по формуле прямоугольников [2. С. 24 - 26]:
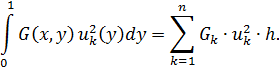
Рассмотрим случай непроницаемости левой границы области фильтрации, т.е. при d=0 при этом уравнение (5) примет вид:
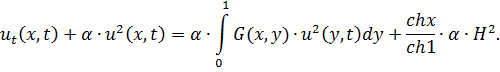
При 
решение этого уравнения равномерно по 
сходится к H-уровню жидкости вне области фильтрации на правой границе.
Приведем пример решения смешанной краевой задачи для обобщенного уравнения Буссинеска с использованием пакета MathCad:
Пусть начальная функция задается в 5 точках и затем интерполируется кубическими сплайнами:
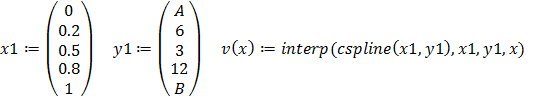
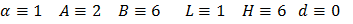
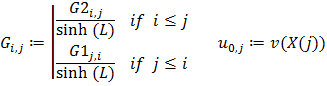
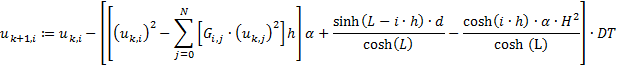
На рис. 1 изображена деформация формы свободной поверхности в случае непроницаемости левой границы области фильтрации и при заданном уровне жидкости на правой границе:
Рис. 1
Здесь жирные сплошные линии – начальная (при t=0) и конечная (по истечении большого промежутка времени t) формы свободной поверхности фильтрующейся жидкости соответственно, остальные – ее промежуточные формы. Из рисунка видно, что начальная форма поверхности с течением времени сходится к константе, которая равна заданному уровню жидкости на правой границе области фильтрации. В данном примере H=6.
Исходя из анализа расчетов и графических представлений движения жидкости со свободной поверхностью в случае непроницаемости левой границы области фильтрации и заданном уровне жидкости на правой границе заметили, что решение интегро – дифференциального уравнения (5) равномерно сходится по x к константе, значение которой равно уровню жидкости H на правой границе области фильтрации.
Библиографический список
1. Фураев В. З. О разрешимости в целом первой краевой задачи для обобщенного уравнения Буссинеска. // Дифференциальные уравнения. 1983. т.19. № 11. С. 2014 – 2015.
2. Фураев В. З., Чухно С. А. К вопросу о численном интегрировании обобщенного уравнения Буссинеска// Краевые задачи и математическое моделирование: сборник материалов VII Всероссийской конференции 4-5 декабря 2004 г. Новокузнецк: Изд-во КемГУ, 2004. С. 24-26.