Информационно-коммуникационные технологии
в педагогическом образовании

ЗНАМЕНИТЫЕ КЛАССИЧЕСКИЕ ЗАДАЧИ ДРЕВНОСТИ

Раздел: Научно-практическая работа студентов педагогического вуза

Журнал: Научно-практическая деятельность студентов педагогического вуза

13 июня 2012 г.

Авторы: Полещук Анастасия Сергеевна

А. С. Полещук

Научный руководитель: Алдакишкина Валентина Владимировна.

ЗНАМЕНИТЫЕ КЛАССИЧЕСКИЕ ЗАДАЧИ ДРЕВНОСТИ

Первые задачи на построение возникли в глубокой древности. Возникли они из хозяйственных потребностей человека. Уже древними архитекторами и землемерами приходилось решать простейшие задачи на построение, связанные с их профессией.

Первые греческие ученые, которые занимались решением геометрических задач на построение, были: Фалес Милетский (624 – 547 гг. до н.э.), Пифагор (ок. 580 – 500 гг. до н.э.), Платон (427 – 347 гг. до н.э.).

Платон и его ученики считали построение геометрическим, если оно выполнилось при помощи циркуля и линейки, то есть путем проведения окружностей и прямых линий. Если же в процессе построения использовались другие чертежные инструменты, то построение не считалось геометрическим. Древние греки вслед за Платоном стремились к геометрическим построениям и считали их идеалом в геометрии.

Уже в древности греческие математики встретились с тремя задачами на построение, которые не поддавались решению с помощью циркуля и линейки. Эти три задачи следующие:

Первая задача. Задача на удвоение куба. Требуется построить ребро куба, который по объему был бы в два раза больше данного куба.

Вторая задача. Задача о трисекции угла. Требуется произвольный угол разделить не три равные части.

Третья задача. Задача о квадратуре круга. Требуется построить квадрат, площадь которого равнялась бы данному кругу.

Они получили название «знаменитых классических задач древности». Над решением этих задач человечество трудилось более двух тысяч лет. Данные задачи составляют увлекательную и поучительную страницу истории.

1. Делосская задача об удвоении куба

Существуют две легенды возникновения задачи об удвоении куба. Приведем одну из них.

Легенда. Царь Минос повелел воздвигнуть памятник своему сыну Главку. Архитекторы дали памятнику форму куба, ребро которого равнялось 100 локтям. Но Минос нашел этот памятник слишком малым и приказал его удвоить. Чувствуя свое бессилие в решении поставленной задачи, архитекторы обратились за помощью к ученым-геометрам, но и они не могли решить указанной задачи.

Попытка решить задачу об удвоении куба при помощи циркуля и линейки

Древние греки сравнительно легко решили задачу об удвоении квадрата.

Обобщая задачу об удвоении квадрата, древние греки перешли к рассмотрению задачи об удвоении куба и стремились решить ее при помощи циркуля и линейки. Оказалось, что решение задачи об удвоении куба сводится к геометрическому построению корня кубического из двух. Действительно, если ребро данного куба положить равным , а ребро искомого куба - , то согласно условию задачи, будем иметь:

откуда.

Однако все старания построить циркулем

и линейкой не увенчались успехом.

Имеет место следующая теорема.

Теорема

Если какой-либо корень приведенного кубического уравнения с рациональными коэффициентами может быть построен посредством циркуля и линейки, то это уравнение обладает, по крайней мере, одним рациональным корнем.

Как уже было показано, задача об удвоении куба сводится к решению кубического уравнения

,

где есть ребро данного куба, - искомое ребро удвоенного куба.

Приняв для простоты длину ребра куба за 1, получим уравнение

.

Это уравнение с рациональными коэффициентами не может иметь рациональных корней. Следовательно, по «теореме неразрешимости», задача об удвоении куба не может быть решена при помощи циркуля и линейки.

Таким образом, задача об удвоении куба и является примером таких задач, которую нельзя решить, прибегая только к циркулю и линейке.

Решение задачи об удвоении куба при помощи вспомогательных средств

Существуют различные оригинальные решения данной задачи с помощью других чертежных инструментов и вспомогательных средств. Приведем решение задачи об удвоении куба, приписываемое Платону. Это решение основано на следующей лемме:

Лемма. Во всякой прямоугольной трапеции с перпендикулярными диагоналями образуют геометрическую прогрессию:

.

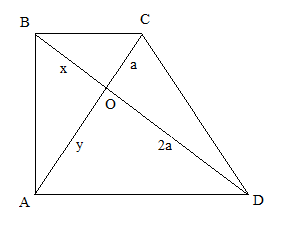Пусть теперь требуется построить так, чтобы , где - ребро данного куба, а - искомое ребро удвоенного куба. Для этого в полученной прогрессии достаточно положить , , , . Тогда будем иметь:

,

откуда ; . Следовательно, или .

и будет ребром удвоенного куба.

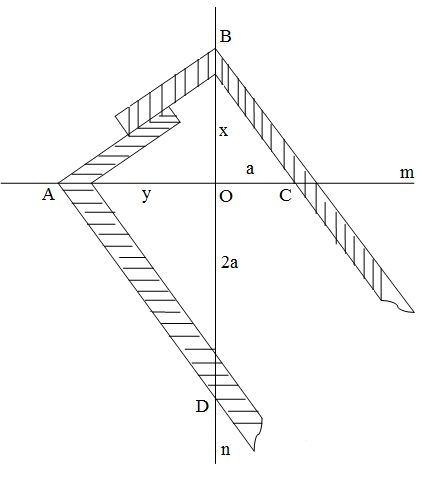
Основываясь на данной лемме, само построение отрезка можно выполнить при помощи двух прямоугольных плотничных наугольников. Это делается следующим образом. Берутся две перпендикулярные прямые и , пересекающиеся в точке . На прямой вправо от точки отложим отрезок , где - сторона куба, подлежащего удвоению.

На прямой вниз от точки отложим отрезок . Теперь берем два прямоугольных плотничных наугольника и располагаем их так, как показано на рисунке, то есть 1) чтобы катет первого наугольника проходил через точку , которая считается данной, а вершина его находилась на прямой ; 2) чтобы катет второго наугольника проходил через точку , которая считается также данной, а вершина находилась бы на прямой ; 3) остальные два катета того и другого наугольника должны соприкасаться.

При таком расположении двух наугольников по данным точкам и найдем на прямых и точки и . Тогда , а . По лемме

, откуда .

Следовательно, и есть построенное ребро удвоенного куба, что и нужно было сделать.

2. Задача о трисекции угла

Вторая древнейшая знаменитая геометрическая задача – это задача о трисекции угла. Возникновение задачи о трисекции угла, в отличие от делосской задачи об удвоении куба, не связано ни с какими преданиями и легендами. Задача о делении угла на три равные части, по-видимому, возникла из потребностей архитектуры и строительной техники. При составлении рабочих чертежей орнаментов, разного рода украшений, многогранных колоннад и так далее, при строительстве, внутренней и внешней отделке храмов, надгробных памятников и других больших и малых сооружений древние инженеры, художники и архитекторы встретились с необходимостью уметь делить окружность на любое конечное число равных частей, а это в некоторых случаях приводило их к рассмотрению трисекции некоторых углов. Делить угол пополам древние греки умели довольно легко, а вот разделить угол на три равные части оказалось не всегда возможно.

Перед учеными встала одна из трудных геометрических проблем, которая стала называться «знаменитой задачей о трисекции угла».

Пользуясь циркулем и линейкой, древние греки умели делить произвольный угол на две равные части. Со времен Пифагора они умели делить прямой угол на три равные части, то есть произвести трисекцию этого угла.

Однако, пользуясь циркулем и линейкой, они смогли выполнить трисекцию углов только для частных случаев.

Доказательства неразрешимости задачи о трисекции произвольного угла при помощи циркуля и линейки

Древнегреческие ученый проявили много тонкого остроумия для изобретения разного рода механизмов, с помощью которых они без особого труда делили произвольный угол на три равные части. Но перед ними всегда стоял вопрос: почему трисекция угла, легко выполнимая при помощи специально изготовленных механизмов, не поддается разрешению при помощи циркуля и линейки?

Обозначим данный угол, который требуется разделить на три равные части, через . Рассмотрим .

Воспользуемся формулами тригонометрии:

После преобразований получаем:

.

Умножая левую и правую части полученного равенства на 2, будем иметь:

Пусть теперь и , тогда

,

или

. (1)

Чтобы доказать, что задача о трисекции угла не разрешима в общем виде, достаточно указать хотя бы один угол, который нельзя разделить при помощи циркуля и линейки. Таким свойством, например, обладает угол в .

Итак, если пользоваться циркулем и линейкой, задача о трисекции угла в общем виде не разрешима.

Решение задачи о трисекции угла при помощи вспомогательных средств

Задача о трисекции угла в общем случае не разрешима при помощи циркуля и линейки, но это вовсе не значит, что данную задачу нельзя решить другими вспомогательными средствами.

Чрезвычайно простое решение задачи дал древнегреческий ученый Архимед. Решает он ее при помощи обыкновенного циркуля и подвижной линейки, на которой разрешается делать две отметки, расстояние между которыми должно равняться радиусу проводимой окружности.

Пусть требуется произвольно взять острый угол разделить на три равные части.

Д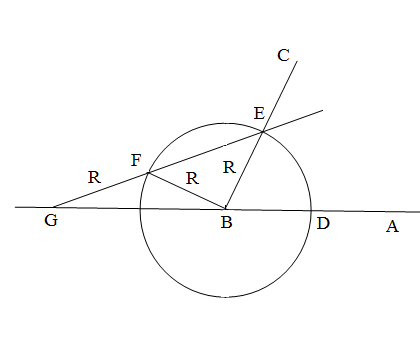ля этого из вершины данного угла , как из центра, произвольным радиусом опишем окружность. Точки пересечения сторон данного угла с окружностью обозначим через и . Теперь берем подвижную линейку с двумя отметками и , причем длина отрезка , и прикладываем ее к точке так, чтобы и оказались на одной прямой с точкой и чтобы находилась на окружности, а - на продолжении стороны . Тогда угол и будет составлять одну треть заданного угла .

3. Задача о квадратуре круга

Задача о квадратуре круга – самая старая из всех математических задач. Она возникла на заре человеческой культуры и ее история охватывает период около четырехсот тысяч лет. Этой задачей раньше греков занимались вавилоняне и египтяне. Независимо от греков ею занимались китайцы и индийцы. Задача о квадратуре круга вместе с тем является самой популярной из всех математических задач. Этой популярности, по-видимому, содействовала ее жизненная необходимость и чрезвычайная простота формулировки, которая доступна как математику, так и нематематику.

Древнегреческие ученые стремились задачу о квадратуре круга решить при помощи циркуля и линейки. Показательна в этом отношении работа Гиппократа Хиосского, которому удалось криволинейную фигуру (гиппократовы луночки) преобразовать в равновеликий ей многоугольник. Однако в рассуждениях Гиппократа Хиосского допущена одна ошибка, которая «из невозможного делает возможным» - неразрешимую задачу о квадратуре круга разрешимой. Поэтому преобразовать круг в равновеликий ему квадрат Гиппократу так и не удалось.

Доказательство невозможности решить задачу о квадратуре круга при помощи циркуля и линейки

Попытки древнегреческих ученых решить задачу о квадратуре круга путем проведения прямых и окружностей так и не увенчались успехом. Дело в том, что задача о квадратуре круга является неразрешимой при помощи циркуля и линейки.

Окончательный удар всем иллюзиям решить задачу при помощи циркуля и линейки был нанесен лишь во второй половине XIX века. Немецкому математику Ф. Линдеману в 1882 году удалось, наконец, вполне строго доказать, что задача о квадратуре круга неразрешима при помощи циркуля и линейки и все старания что-нибудь сделать в этом направлении указанными средствами являются совершенно напрасными и ненужными.

Пусть дан круг радиуса и требуется построить квадрат, равновеликий этому кругу. Обозначим сторону искомого квадрата через , тогда будем иметь:

,

откуда

.

Таким образом, вопрос о построении квадрата, равновеликого данному кругу, сводится к построению произведения данного отрезка на данное число , причем это построение надо провести при помощи только циркуля и линейки.

В теории геометрических построений установлено, что данный отрезок можно умножить при помощи циркуля и линейки на вещественное число лишь только в том случае, если это вещественное число может быть корнем алгебраического уравнения с целыми коэффициентами, разрешимого в квадратных радикалах. Число, которое не может являться корнем никакого алгебраического уравнения с целыми коэффициентами, принято называть трансцендентным числом

Заслуга Ф. Линдемана как раз и заключается в том, что он впервые в мировой науке вполне строго доказал, что есть число трансцендентное и тем самым окончательно установил невозможность решения задачи о квадратуре круга с помощью циркуля и линейки. Вот почему Ф. Линдемана называют «победитель числа ».

Решение задачи о квадратуре круга при помощи вспомогательных средств.

Известно, что задача о квадратуре круга неразрешима при помощи циркуля и линейки. Однако задача о квадратуре круга становится вполне разрешимой, если специально для нее расширить средства построения. Это знали еще древние греки. Они знали, что квадратура круга будет вполне разрешимой, если в процессе построения воспользоваться некоторыми специальными кривыми. Первое такое решение задачи о квадратуре круга еще в VI в. до н.э. выполнил Динострат. Он при своем решении воспользовался квадратрисой. Суть этого метода заключается в следующем.

П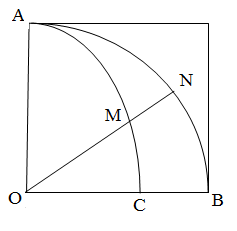усть - четверть окружности, расположенной в квадранте (Квадрант плоскости — любая из 4 областей (углов), на которые плоскость делится двумя взаимно перпендикулярными прямыми, принятыми в качестве осей координат), а - квадратриса этого квадранта. Далее Динострат воспользовался соотношением, которое позднее было доказано Паппом Александрийским:

,

где - конечная точка квадратрисы.

Поскольку , то , или

Откуда длина окружности радиуса равняется . Таким образом, длина окружности определена. Чтобы построить квадрат, равновеликий кругу, Динострат, по-видимому, воспользовался теоремой: площадь круга равна площади треугольника, основание которого равно окружности, а высота – радиусу.