Информационно-коммуникационные технологии
в педагогическом образовании

МЕТРИЧЕСКИЕ ЗАДАЧИ СТЕРЕОМЕТРИИ

Раздел: Научно-практическая работа студентов педагогического вуза

Журнал: Научно-практическая деятельность студентов педагогического вуза

13 июня 2012 г.

Авторы: Салтыкова О. Н.

О. Н. Салтыкова

Научный руководитель: Алдакишкина Валентина Владимировна.

МЕТРИЧЕСКИЕ ЗАДАЧИ СТЕРЕОМЕТРИИ

Необходимость построения изображений различных фигур на плоскости возникла еще в далекой древности. Уже в те времена изображения пространственных форм начинали приобретать важное значение. В современном мире оно существенно возросло. Различного рода чертежи, рисунки, фотографические изображения так широко употребляются в науке, технике, искусстве, быту, что нет необходимости специально говорить об этом.

К изображениям предъявляются различные требования. В одних случаях важно, чтобы изображение обладало наглядностью, т. е. чтобы оно вызывало у нас правильное представление о форме изображенной фигуры; в других - чтобы изображение давало возможность судить об определенных геометрических свойствах этой фигуры; в иных случаях необходима измеримость изображения и т. д.

Для того, чтобы всякое изображение было способно удовлетворить перечисленным требованиям, нужно строить его по определенным законам, имеющим под собой твердую научную основу. Такую основу дает геометрия, а соответствующие закономерности в построении изображений пространственных фигур реализуются с помощью метода проектирования. Изображение, выполненное по методу проектирования, принято называть проекционным.

Знание правил построения проекционных чертежей, понимание значения проекционного чертежа, умение целесообразно и в нужной мере использовать его в педагогическом процессе – вот что необходимо каждому, кто предполагает преподавать математику в школе.

При изображении фигур на плоскости обычно используется параллельное проектирование. Во всех учебных пособиях изображение плоских и пространственных фигур дано именно в этой проекции и при решении задач в курсе геометрии наиболее часто встречается параллельное проектирование.

Допустим, что при центральном проектировании точек плоскости π на плоскость π’ в качестве центра проекций выбрана некоторая бесконечно удалённая точка (не принадлежащая плоскости π’). Тогда проектирующие прямые окажутся параллельными между собой (рис. 1) и мы имеем параллельное проектирование как частный случай центрального.

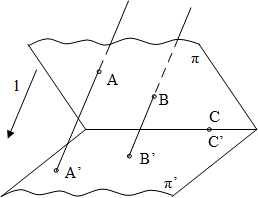
Рис. 1

Множество F0 = f (F’) называется проекцией фигуры F на плоскость π при параллельном проектировании f: F → F’ на плоскости π.

Свойства параллельного проектирования.

1. Прямые линии проектируются в прямые либо в точки.

2. Параллельные прямые проектируются в параллельные прямые, т. е. параллельные прямые в пространстве изображаются на проекционном чертеже параллельными либо совпадающими прямыми (рис. 2).

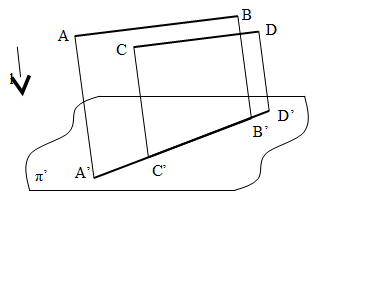
Рис. 2

1. Параллельное проектирование сохраняет отношение трех точек на прямой.

2. Отношение параллельных отрезков равно отношению их проекций.

3. Если отрезки АВ и CD принадлежат одной прямой и A’B’, C’D’ – их проекции, то АВ: CD = A’B’: C’D’.

Следствия:

1. Середина отрезка переходит в середину отрезка.

2. Медиана треугольника переходит в медиану.

3. Биссектриса внутреннего угла треугольника не проектируется в биссектрису.

4. Высота треугольника в общем случае не переходит в высоту.

Все эти свойства используются при решении метрических задач, связанных с плоскими фигурами.

Пусть π’ – некоторая плоскость. Любая фигура F’, принадлежащая этой плоскости, являющаяся проекцией фигуры F и подобная фигуре F0, называется изображением фигуры F на плоскости π’.

Приведем две теоремы необходимые для правильного изображения пространственных фигур.

Теорема Польке-Шварца. Любой плоский четырехугольник А1В1С1D1 вместе с его диагоналями может быть параллельной проекцией тетраэдра ABCD произвольной формы, если только вершины четырехугольника не все лежат на одной прямой.

Теорема Польке. Любые три выходящие из одной точки отрезка, заданные на плоскости, можно принять за параллельную проекцию трех равных, взаимно перпендикулярных и выходящих из одной точки отрезков, расположенных в пространстве.

К чертежам пространственных фигур будем предъявлять три требования. Чертеж должен быть: а) верным; б) наглядным; в) свободно выполненным.

Чтобы выполнить первое требование, достаточно строить изображения в строгом соответствии с законами параллельного проектирования.

Требование второе обязывает нас из многочисленных параллельных проекций данной фигуры выбрать те, которые наилучшим образом говорят нам об особенности формы изображенной фигуры, о взаимном расположении интересующих нас ее элементов.

Всякая точка будет называться заданной на проекционном чертеже, если на нем изображена сама эта точка и ее параллельная проекция на некоторую плоскость, которую будем называть основной. Проекцию точки на основную плоскость будем называть также ее основанием.

Проектирующая прямая, равно как и всякая другая, ей параллельная, определяет направление проектирования точек на основную плоскость. Условимся называть это проектирование внутренним. Внутреннее проектирование может быть как параллельным, так и центральным.

Плоскость, проходящую через проектирующую прямую, будем называть проектирующей. Две проектирующие прямые (несовпадающие) определяют единственную проектирующую плоскость.

Изображение всякой фигуры на проекционном чертеже будем называть полным, если каждая точка этой фигуры является заданной.

К метрическим относятся задачи, связанные с определением истинных (натуральных) величин расстояний, углов и плоских фигур на проекционном чертеже. Можно выделить четыре группы метрических задач.

1. Группа задач, включающих в себя определение расстояний от точки до другой точки; от точки до прямой; от точки до плоскости; от точки до поверхности; от прямой до другой прямой; от прямой до плоскости; от плоскости до плоскости. Причем расстояние от прямой до плоскости и между плоскостями измеряется в тех случаях, когда они параллельны.

2. Группа задач, включающая определение углов между пересекающимися или скрещивающимися прямыми, между прямой и плоскостью, между плоскостями (определение величины двухгранного угла).

3. Группа задач, связанная с определением истинной величины плоской фигуры и части поверхности (развертки).

4. Группа задач на построение биссектрис углов, биссекторных плоскостей, общего перпендикуляра двух скрещивающихся прямых и т. п.

В курсе геометрии для решения подобных задач используются два основных метода:

1. Вычислительный;

2. Строится выносной чертеж-оригинал и используется теорема Фалеса.

Для решения метрических задач проекционный чертеж должен обладать свойством полноты. Однако полный чертеж еще не определяет метрические свойства оригинала. Для того, чтобы чертеж обладал также и метрической полнотой или, как говорят, метрической определенностью, надо добавить к нему условия, которым должен удовлетворять оригинал. Такой чертеж, сопровождающийся условиями, наложенными на оригинал, называется условным. Так, например, из условий задачи может быть известно, что тот или иной параллелограмм является изображением квадрата, или, что пирамида, изображенная на чертеже, в оригинале представляет собой правильный тетраэдр. Если чертеж обладает свойством полноты, то для его метрической определенности достаточно, чтобы была определена форма какого-либо тетраэдра, изображенного на чертеже.

При ортогональном проектировании для построения не просто изображения, например, пирамиды, а пирамиды, на которую наложены определенные метрические условия, используются следующие свойства пирамид:

1. Если в пирамиде все боковые ребра равны или боковые ребра образуют с плоскостью основания равные углы, то высота пирамиды проектируется в центр окружности, описанной около основания.

2. Если все боковые грани пирамиды наклонены к плоскости основания под одним и тем же углом, то высота пирамиды проектируется в центр вписанной в основание окружности.

Рассмотрим несколько задач.

Задача 1. В прямоугольном треугольнике АВС С = 900, АВ = 5, АС = 2. На изображении этого треугольника построить изображение центра вписанной окружности и точек касания.

Решение. Решить эту задачу проще, используя теорему Фалеса.

Построим выносной чертеж-оригинал. Сначала найдем катет ВС. По теореме Пифагора ВС = . Строим треугольник АВС по двум катетам АС и ВС (рис. 3).

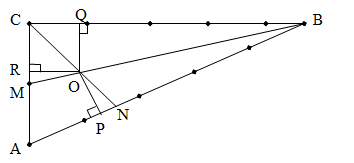
Рис. 3

Известно, что центром вписанной в треугольник окружности является точка пересечения его биссектрис. Построим в треугольнике АВС биссектрисы BM и CN. Они пересекутся в точке О, являющейся центром вписанной окружности. По свойствам параллельного проектирования BN: NA = B’N’: N’A’, AM: MC = A’M’: M’C’. С помощью вспомогательного луча l, на котором откладываем отрезки A’M0 и М0С0 (A’M0 = АМ, М0С0 = МС), строим на изображении A’B’C’ треугольника АВС точку M’ и затем прямую B’M’ – биссектрисы ВМ (рис. 4). Аналогично, строим изображение биссектрисы СN – прямую C’N’. Точка О’ пересечения прямых B’M’ и C’N’ – искомое изображение центра окружности, вписанной в треугольник АВС.

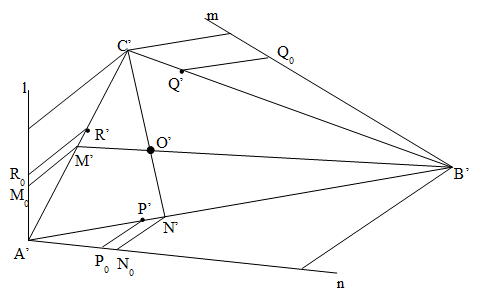
Рис. 4

Теперь построим изображения точек касания. Для этого сначала получим их на чертеже-оригинале, опустив из точки О перпендикуляры на стороны треугольника АВС (рис. 3). По свойствам параллельного проектирования АР: РВ = A’P’: P’B, BQ: QC = B’Q’: Q’C’, AR: RC = A’R’: R’C’. Используя эти отношения, аналогично тому, как мы строили точку M’, построим точки P’, Q’, R’ на сторонах треугольника A’B’C’ (рис. 4). Они и дадут искомые изображения точек касания.

Задача 2. Дано изображение конуса, усеченного плоскостью SAB, проходящей через вершину конуса. Высота конуса в 1,5 раза больше диаметра основания. Требуется построить истинный вид фигуры сечения.

Решение. Проводим произвольный диаметр M’N’ основания конуса (рис. 5). При помощи параллельной ему хорды, разделенной в точке К’ пополам, находим направление K’O’, перпендикулярное в оригинале к диаметру M0N0. Касательные в точках М’ и N’ диаметра должны быть проведены параллельно прямой K’O’. В оригинале они также перпендикулярны к диаметру М0N0.

Чтобы найти положение точек А’ и В’ в оригинале, проводим через эти точки прямые: А’А’’||B’B’’||K’O’. В пересечении с окружностью эти прямые определяют нам точки А’’ и В’’, соответствующие точкам А’ и В’ чертежа.

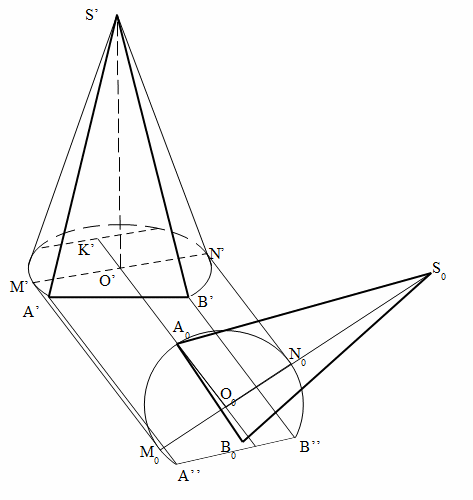
Рис. 5

Далее переходим к определению истинной длины образующей конуса. Это можно сделать, рассматривая образующую как гипотенузу прямоугольного треугольника, у которого одним катетом служит радиус основания, а другим высота конуса. По условию задачи высота конуса в 1, 5 раза больше диаметра, а значит, в 3 раза больше радиуса. Примем за первый катет отрезок А0O0, изображающий истинную длину радиуса. Тогда не сложно построить и второй катет O0S0 = 3O0A0. Получаем треугольник А0O0S0, гипотенуза A0S0 которого и дает истинную длину образующей.

Теперь строим треугольник A0B0S0 по трем сторонам (S0B0 = S0A0, A0B0 = A’’B’’). Этот треугольник и представляет истинную форму сечения.

Задача 3. Дана правильная четырехугольная пирамида SABCD, у которой SA = = AB = 1. К – центр грани SCD. Вычислить угол между прямыми AS и ВК.

Решение. Решим задачу векторно-координатным методом.

Введем прямоугольную систему координат как показано на рисунке 6. Примем отрезок ОА за единичный. Тогда координаты точек: , , , . Теперь найдем координаты векторов: , .

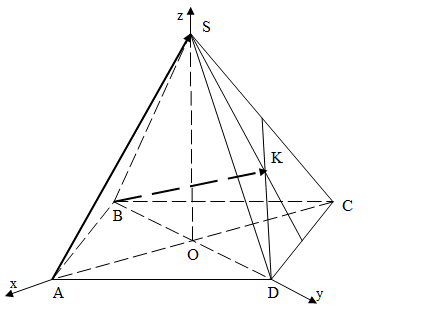
Рис. 6

.

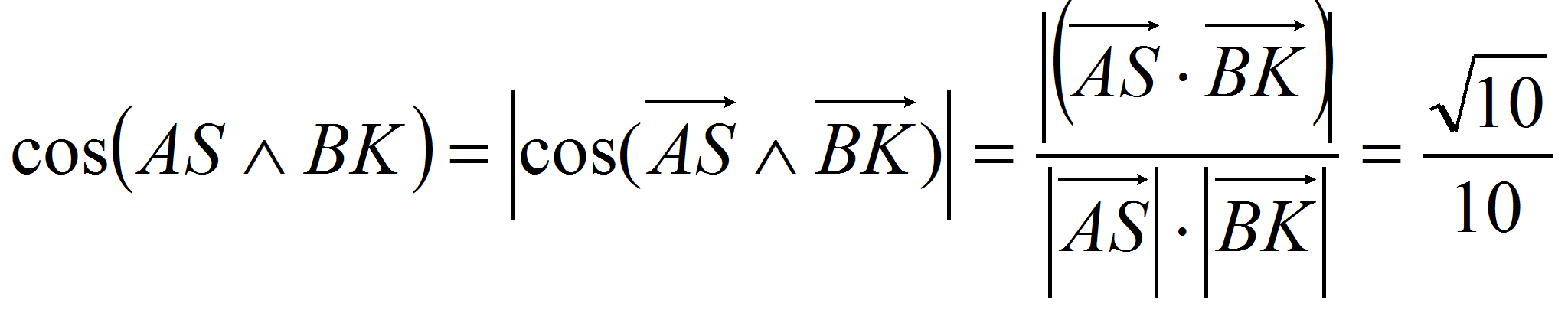Ответ: .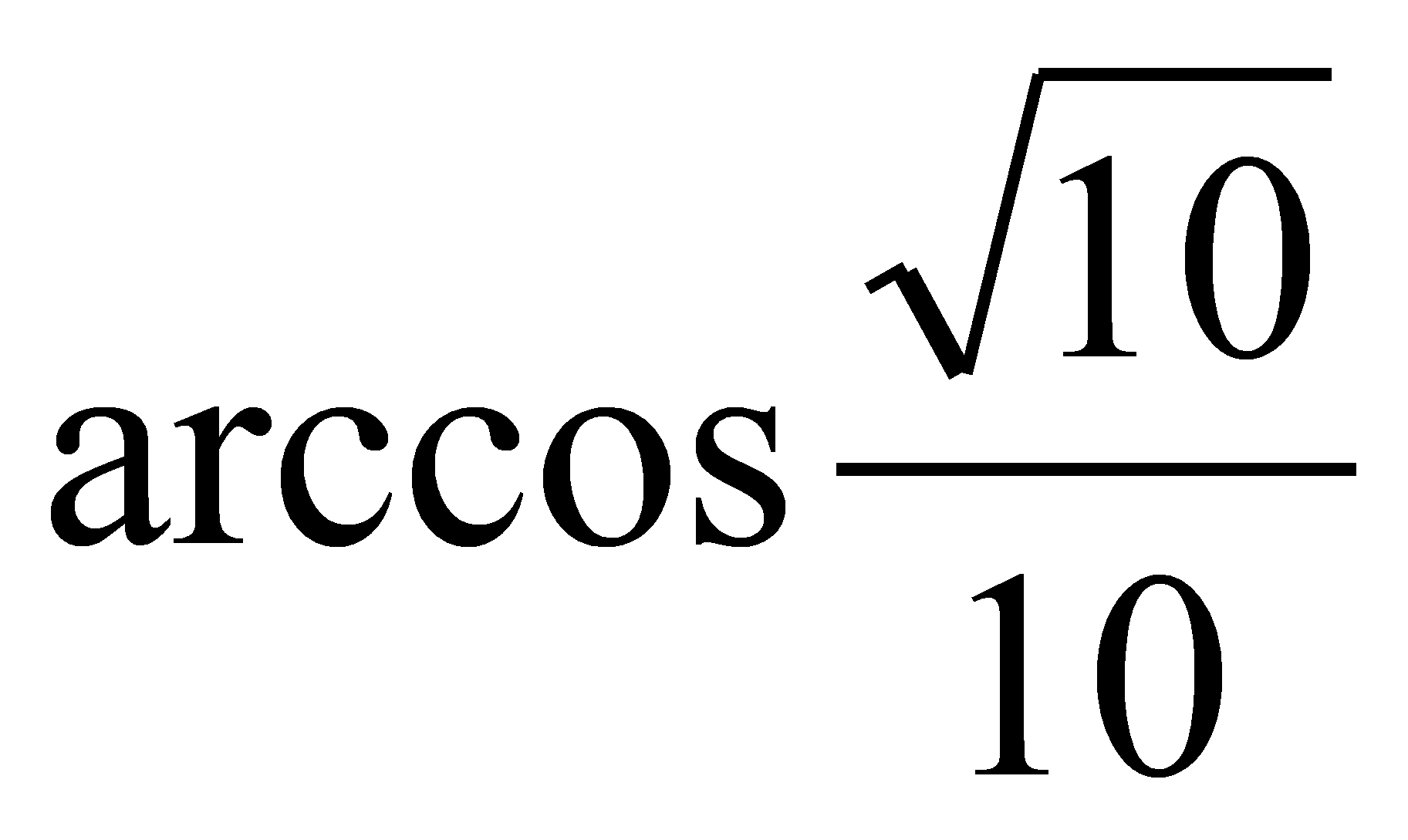

Задача 4. Дан куб ABCDA1B1C1D1. Из точки С опустить перпендикуляр на плоскость A1BD.

Решение. С1А1ВD – правильный тетраэдр (рис. 7), так как все его ребра являются диагоналями равных квадратов (граней куба). Построим его высоту С1К, учитывая, что точка К – это точка пересечения медиан треугольника, лежащего в основании тетраэдра. Полученная высота определит направление искомого перпендикуляра.

Прямая C1К перпендикулярна прямой А1N. Проведем через точку С прямую параллельно прямой С1К. Она пересечет прямую А1N в точке Н.

Прямая СН – искомый перпендикуляр.

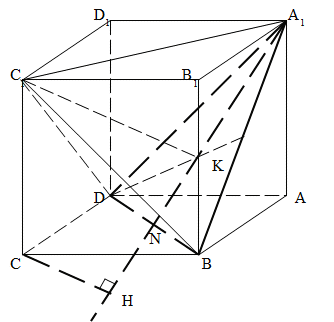
Рис. 7