ИСПОЛЬЗОВАНИЕ ВНЕВПИСАННОЙ ОКРУЖНОСТИ ДЛЯ ПОВЫШЕНИЯ КАЧЕСТВА ПОДГОТОВКИ К ЕГЭ
Раздел: Теория и практика обучения школьников
Журнал: Проблемы модернизации образования в XXI веке
29 ноября 2016 г.
Авторы: Филиппова Татьяна Евгеньевна
Т. Е. Филиппова
T. E. Filippova
ИСПОЛЬЗОВАНИЕ ВНЕВПИСАННОЙ ОКРУЖНОСТИ ДЛЯ ПОВЫШЕНИЯ КАЧЕСТВА ПОДГОТОВКИ К ЕГЭ
USE OF THE ESCRIBED CIRCLE FOR IMPROVEMENT OF QUALITY OF PREPARATION FOR THE EGE
Аннотация. Данная статья будет интересна в первую очередь учителям математики, осуществляющим подготовку учащихся к ЕГЭ по математике на профильном уровне. В школьной программе свойствам окружности уделяется незначительное время и внимание, а про вневписанную окружность и не упоминается. Материал статьи поможет восполнить этот пробел на требуемом уровне.
Annotation. This article will be of interest primarily to teachers of mathematics who are carrying out training of pupils for the Unified State Examination in mathematics at the profile level. In the school program of the circle properties is given little time and attention, and about escribed circle not mentioned. Material of article will help to meet this lack at the required level.
Следует отметить, что действующие школьные программы по математике не предусматривают изучение понятия вневписанной окружности треугольника. Однако с ним полезно познакомиться, так как решение некоторых задач ЕГЭ по математике, связано с использованием этого понятия. Сделать это возможно в рамках работы факультативного или элективного курса.
При этом будет достигнуто несколько целей, учитель сможет:
- систематизировать, расширить и углубить знания о вневписанной окружности;
- развить умение анализировать, сравнивать и делать выводы;
- повысить уровень понимания и практической подготовки в таких вопросах, как решение геометрических задач с помощью алгебры.
Для достижения этих целей потребуется решить такие задачи:
- применить аппарат алгебры к решению геометрических задач;
- применить свойство геометрических преобразований к решению задач;
- овладеть рядом интеллектуальных умений на уровне свободного их использования;
- оценить свой потенциал с точки зрения образовательной инициативы.
Разумеется, сначала следует дать определение вневписанной окружности.
Вневписанной окружностью треугольника называется окружность, касающаяся одной из его сторон и продолжений двух других.
Для каждого треугольника существует три вневписанных окружности, которые расположены вне треугольника, почему они и получили название вневписанных.
Центральное место в геометрии треугольника занимают свойства так называемых замечательных точек и линий. Три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке – центре описанной около треугольника окружности. Биссектрисы трех внутренних углов треугольника пересекаются в одной точке – центре вписанной в треугольник окружности. Если рассмотреть дополнительно биссектрисы трех пар внешних углов треугольника, то получаются еще три замечательных точки – центры вневписанных окружностей.
В XV- XVI веках появилось огромное количество исследований свойств треугольника. Эти исследования составили большой раздел планиметрии, получивший название «Новая геометрия треугольника». Вот одна из замечательных теорем того времени, принадлежащая Л. Эйлеру: «Середины сторон треугольника, основания его высот и середины отрезков высот от вершины до точки их пересечения лежат на одной окружности». Она обычно называется окружностью девяти точек (по количеству замечательных точек, через которые она проходит).
Если позволяют временные возможности, полезно рассмотреть теоремы с доказательствами, связанные с понятием вневписанной окружности, при ограниченном времени доказательства можно пропустить.
Теорема 1. Биссектриса внутреннего угла ВАС треугольника АВС и биссектрисы двух внешних углов при вершинах В и С пересекаются в одной точке.
Доказательство: Проведем внешние биссектрисы из вершин В и С. Пусть они пересекаются в точке Оа. Докажем, что биссектриса угла ВАС проходит через точку Оа. Все точки биссектрисы СОа равноудалены от сторон угла, значит, расстояние от точки Оа до прямых ВС и АС равны, так как Оа лежит на биссектрисе угла ВСК1, то есть ОаК1=ОаК3.
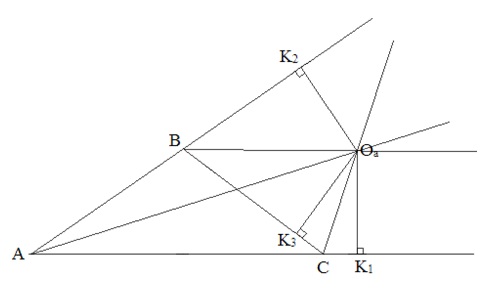
Рисунок 1. Чертеж к доказательству теоремы 1
Аналогично, равны расстояния от точки Оа до прямых ВС и АВ - ОаК2 = ОаК3 . Тогда очевидно, что точка Оа равноудалена от прямых АС и АВ, то есть лежит на биссектрисе угла ВАС.
Из теоремы 1 следует существование окружности с центром в точке Оа, касающейся прямых АС, АВ и ВС. Данную окружность и называют вневписанной окружностью.
Таким образом, шесть биссектрис треугольника – три внутренние и три внешние – пересекаются по три в четырех точках – центрах вписанной и трех вневписанных окружностей.
Радиусом вневписанной окружности является отрезок перпендикуляра, проведенного из центра окружности к какой-либо стороне треугольника или ее продолжению.
Теорема 2. Пусть K1 – точка касания вневписанной окружности с продолжением стороны AC треугольника ABC. Тогда длина отрезка AK1 равна полупериметру треугольника ABC.
Доказательство: Пусть точки K2 и K3 – точки касания вневписанной окружности с прямыми AB и BC соответственно. Тогда СК1 = СК3, ВК2 = ВК3 и периметр треугольника АВС равен 2р = АС + СВ + АВ = АС + СК3 + ВК3 + АВ = АС + СК1 + АВ + ВК2 = АК1 + АК2. А так как АК1 =АК2, то р = АК1, что и требовалось доказать.
Утверждение: Пусть S, p, a, b, c, соответственно, – площадь, полупериметр и стороны некоторого треугольника, а ra, rb, rc – радиусы вневписанных окружностей, тогда справедливы равенства
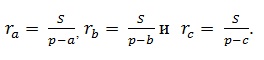
Доказательство: Центром окружности, вписанной в угол А, служит точка Оa (точка пересечения биссектрис внешних углов треугольника, не смежных с углом А; радиус этой окружности есть отрезок перпендикуляра, проведенного из точки Оa к какой-либо стороне треугольника (или ее продолжению):
![]()
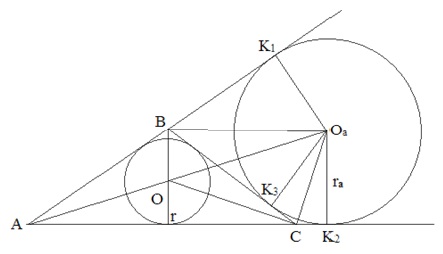
Рисунок 2. Чертеж к доказательству теоремы 2
Аналогично можно найти центры Ob, Oc и радиусы двух других вневписанных окружностей.
Зная длины сторон a,b, c треугольника ABC, можно вычислить длины ra, rb, rc.
Действительно,
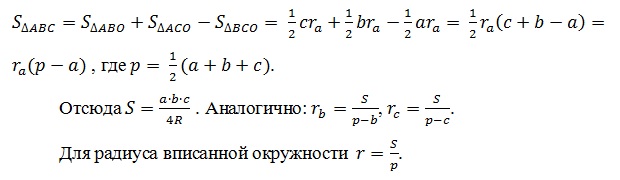
Рассмотрим примеры применения вневписанной окружности при решении задач.
1. Задачи на построение
Задача 1.1. Построить треугольник по периметру и двум углам.
Дано: Углы α и β, периметр треугольника P.
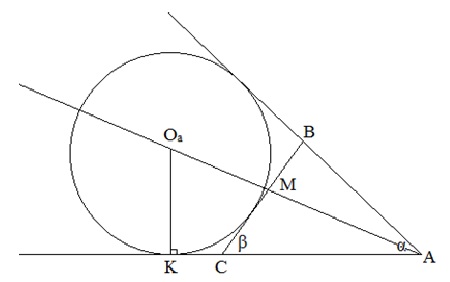
Рисунок 3. Построение треугольника по периметру и двум углам
Построение.
- Построить отрезок, равный полупериметру (АК).
- Из точки А построить данный по условию угол α , а из точки К восстановить перпендикуляр.
- Построить биссектрису угла САВ.
- Построить окружность с центром в точке пересечения биссектрисы угла А с перпендикуляром ОаК и радиусом ОаК.
- На отрезке АК построить второй данный угол β так, чтобы его луч был касательной к окружности.
- Данная касательная пересечет вторую сторону угла в точке В.
∆ABC – искомый треугольник, следуя из Теоремы 1.
Задача 1.2. Постройте треугольник, если дана сторона, противолежащий ей угол треугольника и сумма двух других сторон.
Решение: Пусть дана сторона a, угол А и сумма сторон b + c. Тогда известна длина полупериметра искомого треугольника
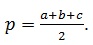
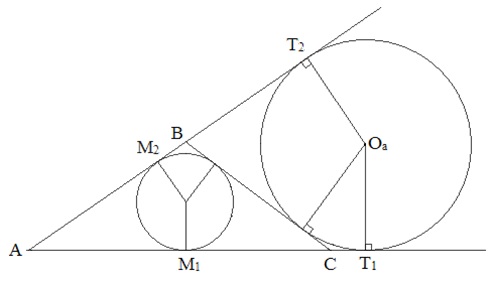
Рисунок 4. Построение треугольника по стороне, противолежащему ей углу и сумме двух других сторон
Значит, известны положения точек T1 и T2 на сторонах угла А. Восстановив перпендикуляры в этих точках к сторонам угла А, на их пересечении получим центр вневписанной окружности, а значит, вневписанная окружность построена.
Расстояние от точки Т1 до точки касания вписанной окружности равно а. Следовательно, мы можем найти точки касания вписанной окружности искомого треугольника со сторонами угла А и построить саму вписанную окружность. Общая внутренняя касательная к построенным окружностям отсекает на сторонах угла искомый треугольник.
2. Задачи на доказательство
Задача 2.1. Две непересекающиеся окружности с радиусами R1 и R2 касаются сторон прямого угла с вершиной А. Общая внутренняя касательная с окружностями пересекает стороны угла в точках В и С. Найти площадь треугольника АВС.
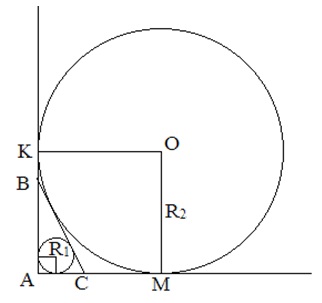
Рисунок 5. Чертеж к решению задачи 2.1
Решение: Так как обе окружности касаются сторон угла, то одна из них будет вписанной в треугольник АВС, а другая вневписанной. Пусть, где R1 и R2 – соответственно радиусы вписанной и вневписанной окружностей (рисунок 5). Если О – центр вневписанной окружности, а точки К и М – точки касания со сторонами угла А. Легко доказать, что АКОМ – квадрат со стороной R2. По теореме 2
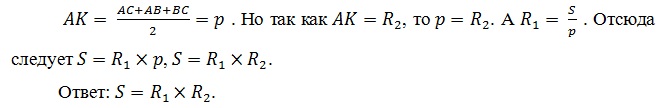
Задача 2.2. К двум непересекающимся окружностям проведены две общие внешние касательные и общая внутренняя касательная. Докажите, что отрезок внутренней касательной, заключенный между внешними касательными, равен отрезку внешней касательной, заключенному между точками касания.
Решение: Пусть даны две окружности. Точки касания окружностей с первой внешней касательной – А и В, со второй – С и D (рисунок 6).
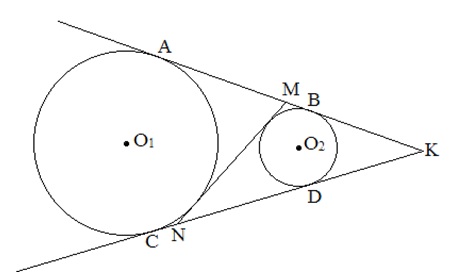
Рисунок 6. Чертеж к решению задачи 2.2
Внутренняя касательная пересекает внешние в точках М и N. Продолжим прямые АВ и СD до их пересечения в точке К. Тогда окружность с центром О2 является вписанной в треугольник МNK, а окружность с центром О1 – вневписанной. Обозначим сторону МN треугольника MNK через а и его полупериметр через р. Тогда (по Теореме 2) АК = р и ВК = р – а. Значит, АВ = а, т. е. АВ = МN. Аналогично CD = MN. Что и требовалось доказать.
В ходе всей работы старшеклассники систематизируют, расширяют и углубляют знания на пересечении алгебры и геометрии, повышают уровень понимания и практической подготовки в таких вопросах, как решение геометрических задач с помощью алгебры. А кроме того, применяют аппарат алгебры к решению геометрических задач и свойство геометрических преобразований к решению задач, что значительно упрощает решение сложных задач, как на построение, так и на доказательство.
Список литературы
- Амелькин, В.В. Геометрия на плоскости: Теория, задачи, решения/ В.В. Амелькин, Т.И Рабцевич, В.Л. Тимохович – М.: «Издательский дом «Оникс» 21 век», 2013. – 591с.
