ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ЭФФЕКТИВНОСТИ ЭЛЕКТИВНОГО ONLINE-КУРСА «РЕАЛЬНАЯ МАТЕМАТИКА» В ПРОЦЕССЕ ПОДГОТОВКИ К ЕГЭ ПО МАТЕМАТИКЕ ПРОФИЛЬНОГО УРОВНЯ
Раздел: Проблемы и перспективы современного физико-математического образования
Журнал: Материалы V Международной научно-практической конференции «Проблемы и перспективы современного образования: практика вуза и школы». Часть 2
19 марта 2021 г.
Авторы: Фомина Анжелла Владимировна , Овечкина Алена Валерьевна
УДК 373.5.016:514
А. В. Овечкина, А. В. Фомина
A. V. Ovechkina, A. V. Fomina
Овечкина Алена Валерьевна, магистрант 2 курса ФИМЭ, НФИ КемГУ, г. Новокузнецк, Россия.
Фомина Анжелла Владимировна, к. ф.-м. н., доцент, НФИ КемГУ, г. Новокузнецк, Россия.
Ovechkina Alena Valerievna, 2-nd year master's student FIME, Novokuznetsk Institute (branch) of «Kemerovo state University», Novokuznetsk, Russia.
Fomina Anzhella Vladimirovna, Candidate of Physical and Mathematical Sciences, Associate Professor, Novokuznetsk Institute (branch) of «Kemerovo state University», Novokuznetsk, Russia.
ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ЭФФЕКТИВНОСТИ ЭЛЕКТИВНОГО ONLINE-КУРСА «РЕАЛЬНАЯ МАТЕМАТИКА» В ПРОЦЕССЕ ПОДГОТОВКИ К ЕГЭ ПО МАТЕМАТИКЕ ПРОФИЛЬНОГО УРОВНЯ
EXPERIMENTAL VERIFICATION OF THE EFFICIENCY OF THE ELECTIVE ONLINE-COURSE «REAL MATHEMATICS» IN THE PROCESS OF PREPARATION FOR THE USE ON MATHEMATICS OF THE PROFILE LEVEL
Аннотация. В статье описывается разработанный элективный online-курс «Реальная математика». Для проверки эффективности применения элективного online-курс в процессе подготовки учеников к ЕГЭ по математике профильного уровня, проводится педагогический эксперимент. Рассмотрены цели и задачи каждого этапа эксперимента, а также представлены их предварительные результаты.
Annotation. The article describes the developed elective online course «Real Mathematics». To test the effectiveness of the use of an elective online course for preparing students for the USE in mathematics of a profile level, a pedagogical experiment is being conducted. The goals and objectives of each stage of the experiment are considered, and their preliminary results are presented.
Ключевые слова: единый государственный экзамен, реальная математика, элективный курс, математика, педагогический эксперимент.
Keywords: unified state examination, mathematics, real mathematics, elective course, pedagogical experiment.
Актуальность исследования заключается в рациональном выборе эффективной формы подготовки выпускников образовательно учреждения по основной общей образовательной программе среднего общего образования для успешного прохождению единого государственного экзамена (ЕГЭ) по математике. Необходимо отметить, что прохождение ЕГЭ по математике является обязательным для всех выпускников образовательных учреждений, с целью определения соответствия результатов освоения обучающимися основной общей образовательной программы с требованиями федерального государственного образовательного стандарта (ФГОС) [2].
Стоить обратить внимание на то, что ЕГЭ по математике подразделяется на два уровня: базовый и профильный, в зависимости от уровня усвоения УУД по учебным предметам алгебра и геометрия, именно поэтому в контрольно измерительных материалах (КИМ) используются наборы заданий разного уровня сложности, которые представлены в стандартизированной форме.
После изучения перечня заданий включенных в КИМ ЕГЭ по математике профильного уровня, а также кодификатора и спецификации и учебно-методических рекомендаций, следует обратить внимание во время подготовки обучающихся к прохождению итоговой аттестации на весьма объемный блок заданий, под названием: «Реальная математика».
Таким образом, при более подробном рассмотрении КИМ ЕГЭ по математике профильного уровня, можно выделить следующие задания из раздела «Реальная математика»:
- задание № 1 – простейшие текстовые задачи на: вычисления; нахождение процентов от числа или числа по его процентам; округление с недостатком или с избытком.
- задание № 11 – текстовые задачи на: проценты, сплавы, смеси; движение по прямой; движение по окружности; движение по воде; задачи на совместную работу; на прогрессии.
- задание № 17 – задачи финансовой математики на: оптимальный выбор; на банки, вклады, кредиты [1].
Следует отметить, что освоение общего подхода к решению данного рода математических задач, по своей сути, является моделью решению бытовых, практических, технических задач, которые будут повседневно встречаться человеку на протяжении всей его жизни. Поэтому немало важным в курсе школьной математики является обучение учащихся решать задачи «Реальной математики» разного уровня сложности. От эффективности применения методов обучения решению задач реальной математики во многом зависит и степень подготовленности школьников к последующей за обучением практической деятельности.
Поэтому для улучшения процесса подготовки выпускников к ЕГЭ по математике профильного уровня, был специально разработан online-курс элективных занятий под названием «Реальная математика», с использованием информационно коммуникационных технологий. Реализация данного курса производилась на платформе оnline-сервиса GoogleClassroom.
Данный online-курс содержит теоретико-методический материал необходимый для того, чтобы научиться успешно решать задачи «Реальной математики» из КИМ ЕГЭ по математике профильного уровня, а также самостоятельные задания для выпускников и итоговые контрольные тестирования к каждому разделу. В нем продемонстрированы не просто решения разного типа задач, которые выявлены из КИМ демонстрационных вариантов ЕГЭ по математике, но и непосредственно сформулированы алгоритмы работы над каждым типом задач.
Время необходимое для реализаций курса 32 часа, оно берется из расчета, что занятия проводятся по 2 часа в неделю.
Перечислим разделы разработанного элективный online-курс «Реальная математика», который применяется в процессе подготовки выпускников к ЕГЭ (профильного уровня): общий подход к решению текстовых задач (ознакомительный); решение задач на округление с недостатком или с избытком; решение задач на нахождение процентов от числа; нахождение числа по его процентам и на процентное соотношение; решение задач на сушку, сплавы, смеси; решение задач финансовой математики; решение задач на совместную работу; решение задач на движение по прямой; решение задач на движение по воде; решение задач на движение по окружности [3].
Для подтверждения эффективности применения специально разработанного online-курс элективных занятий под названием «Реальная математика» в процессе подготовки учащихся старшего класса профильной направленности, был проведен педагогический эксперимент.
Ниже представлены этапы педагогического эксперимента с указанием его продолжительности, цели каждого этапа и его задачи.
- Констатирующий этап – время его проведения 1 неделя, его целью является – получение данных с помощью тестирования, которые позволят выявить уровень знаний и умений старшеклассников, необходимых для усвоения содержания элективного курса «Реальная математика».
Задачи констатирующего этапа:
а) Выбор класса для проведения эксперимента и деление его на 2 подгруппы (экспериментальную и контрольную).
б) Проведение работы по оцениванию уровня знаний и умений учащихся подгрупп при решении задач «Реальной математики».
Необходимо отметить, что по итогам тестирования ученики в экспериментальной и контрольной группах обладают очень близкими результатами. - Формирующий этап – отведено 4 месяца, целью является - внедрение разработанных материалов элективного online-курс «Реальная математика» для подготовки выпускников к сдаче ЕГЭ по математике в учебный процесс.
Задачами формирующего этапа является:
а) Реализация элективного online-курс «Реальная математика» для подготовки выпускников к сдаче ЕГЭ по математике в экспериментальной подгруппе.
б) Наблюдение за ходом и промежуточными результатами в процессе реализации online-курс «Реальная математика» для подготовки выпускников к сдаче ЕГЭ по математике профильного уровня, для дальнейшего уточнения, улучшения содержания элективных курсов и методических рекомендаций по его использованию. - Контрольный этап – затрачивается 2 недели, его цель – проверить гипотезу исследования – действительно ли разработанные нами элективный курс и методика его реализации способствуют повышению качества знаний.
Задачами контрольного этапа является:
а) Проведение повторного оценивания уровня знаний учащихся по заданиям ЕГЭ по математике (профильного уровня) курса «Реальная математика» в двух группах: контрольной и экспериментальной.
б) Сопоставление результатов с первоначальными данными.
Стоит уточнить, что количество учеников в контрольной и экспериментальной группах одинаковое и равно 12.
На диаграмме (рис. 1) представлено соотношение количества человек в каждой группе, успешно справившихся с итоговыми тестами по отдельным, пройденным на данный момент времени, разделам разработанного элективного online-курса «Реальная математика», эти ученики дали правильные ответы в диапазоне от 85 % до 100 %.
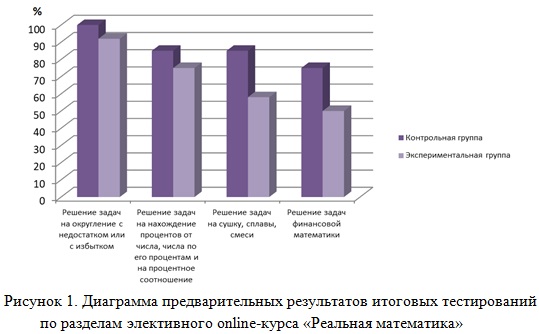
Данная диаграмма наглядно показывает, что в экспериментальной группе ученики лучше справляются с итоговыми тестированиями, исходя из этого, можно сделать вывод о том, что разработанный элективный online-курс «Реальная математика» будет эффективен в процессе подготовки учащихся к ЕГЭ по математике профильного уровня.
Список литературы
- Сайт Федерального института педагогических измерений ФИПИ [Электронный ресурс]. – Москва, 2020. – Режим доступа: http://www.fipi.ru.
- Федеральный закон от 29.12.2012 № 273-ФЗ «Об образовании в Российской Федерации» (ред. от 02.12.2019)
- Ященко И.В., Рослова Л.О., Высоцкий И.Р., Семенов А.В. Методические рекомендаций для учителей подготовленные на основе анализа типичных ошибок участников ЕГЭ 2019 года по математике / И.В. Ященко, Л.О. Рослова, И.Р. Высоцкий, А.В. Семенов. – М.: ФИПИ, 2019.
