Информационно-коммуникационные технологии
в педагогическом образовании

ИСПОЛЬЗОВАНИЕ ОБОБЩЕННОГО МЕТОДА ИНТЕРВАЛОВ ПРИ РЕШЕНИИ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ

Раздел: Проблемы и перспективы современного физико-математического образования

Журнал: Проблемы и перспективы современного физ.-математ. и цифрового образования. Ч.1

31 марта 2020 г.

Авторы: Осипова Людмила Александровна , Гридчина Валентина Борисовна

УДК 372.851

В. Б. Гридчина, Л. А. Осипова

V. B. Gridchina, L. A. Osipova

Гридчина Валентина Борисовна, кандидат педагогических наук, доцент, НФИ КемГУ, г. Новокузнецк, Россия.
Осипова Людмила Александровна, кандидат педагогических наук, доцент, НФИ КемГУ, г. Новокузнецк, Россия.

Gridchina Valentina Borisovna, candidate of pedagogical Sciences, associate Professor, NFI KemGU, Novokuznetsk, Russia.
Osipova Ludmila Alexandrovna, candidate of pedagogical Sciences, associate Professor, NFI KemGU, Novokuznetsk, Russia.

 

ИСПОЛЬЗОВАНИЕ ОБОБЩЕННОГО МЕТОДА ИНТЕРВАЛОВ ПРИ РЕШЕНИИ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ

USE OF THE GENERALIZED INTERVAL METHOD IN RESOLVING IRRATIONAL INEQUALITIES

 

Аннотация. В статье рассматривается обобщенный метод интервалов решения неравенств, приводится алгоритм его использования. На конкретных примерах авторы демонстрируют возможность использования данного метода при решении иррациональных неравенств, указывая достоинства и недостатки данного метода.

Annotation. The article considers a generalized method of intervals for solving inequalities, provides an algorithm for its use. Using specific examples, the authors demonstrate the possibility of using this method in solving irrational inequalities, indicating the advantages and disadvantages of this method.

Ключевые слова: обобщенный метод интервалов, иррациональные неравенства, равносильные преобразования неравенств.

Keywords: generalized interval method, irrational inequalities, equivalent transformations of inequalities.

 

Иррациональными называют неравенства, в которых переменная содержится под знаком корня. Основной метод решения иррациональных неравенств – метод равносильных преобразований. Так, например, неравенство  равносильно совокупности двух систем неравенств: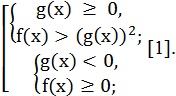 [1].

Однако учащиеся не всегда помнят условия равносильного перехода. Например то, что возводить обе части неравенства в квадрат можно только в случае, когда обе части неравенства неотрицательны. Часто учащиеся забывают рассмотреть второй случай, когда правая часть неравенства отрицательна. Альтернативой методу равносильных преобразований при решении иррациональных неравенств может служить обобщённый метод интервалов.

Приведем алгоритм решения неравенств обобщенным методом интервалов. Пусть требуется решить неравенство F(x) ˅ 0, где ˅- один из знаков <, >, ≤, ≥.

1. Найти область определения функции y = F(x) (область допустимых значений неравенства).
2. Разложить F(x), если это возможно, на множители.
3. Найти нули функции, решив уравнение F(x) = 0.
4. Отметить на числовой прямой область определения и нули функции y = F(x).
5. Определить знак функции y = F(x) на каждом из полученных промежутков и записать ответ.

При решении неравенства обобщенным методом интервалов используется одна числовая прямая и, чтобы не загромождать чертеж излишними деталями, мы предлагаем следующую технику изображения области определения и нулей функции.

На числовой прямой обозначаем область определения функции, отмечая ее границы вертикальными чертами со штриховкой в ту сторону, где функция не определена (так называемые «запретные зоны»). Если граничная точка не входит в область определения, то отмечаем ее пустой (выколотой). Далее наносим на числовую прямую нули функции. В результате область определения функции разбивается на промежутки, внутри каждого из которых функция y = F(x) сохраняет знак. Определяем знак функции на каждом промежутке. При записи ответа выбираем промежутки нужного знака, не забывая, в случае нестрогого неравенства, про отдельно стоящие закрашенные точки (нули функции).

Рассмотрим несколько примеров, демонстрирующих использование данного метода.

Пример 1. Решить неравенство: > 8 - 2x [2].

Решение. Введем функцию F(x) = - (8 - 2x).

Найдем область определения функции, решив неравенство: -x² + 6x - 5 ≥ 0.

Получим D(f) = [1; 5].

Запишем неравенство в виде - (8 - 2x) > 0.

Найдем нули функции, решив уравнение - (8 - 2x) = 0.

Иррациональное уравнение = (8 - 2x), равносильно системе:

Уравнение имеет два корня: x = 3 и x = 4,6. Второй корень не удовлетворяет неравенству x ≤ 4, следовательно, решение системы x = 3.

На числовой прямой обозначим область определения функции и нуль функции x = 3. На каждом из полученных промежутков определим знак функции F(x) (рис. 1).

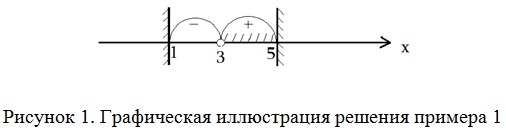
Ответ: (3; 5).

Пример 2. Решить неравенство: ≤ 0.

Решение. Рассмотрим функцию F(x) = .

Найдем область определения функции из условия x² - 1 ≥ 0.

Получим D(f) = .

Запишем неравенство в виде ≤ 0.

На числовой прямой обозначим область определения и нули функции: x = -2; -1; 1. Число x = 0 не отмечаем, так как оно попадает в промежуток, на котором функция не определена.

На каждом из трех промежутков определим знак функции F(x) (рис. 2).

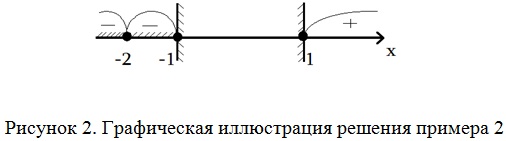
При записи ответа не забываем включить в него x = 1.

Ответ: .

Пример 3. Решить неравенство: [2].

Преобразуем неравенство к виду: .

Введем функцию F(x) =  и найдем ее область определения:

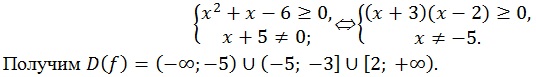
Найдем нули функции, решив уравнение + 2x + 8 = 0 или

= -(2x + 8). Уравнение равносильно системе:

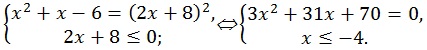
x = -7 решение системы,  посторонний корень.

На числовой прямой отметим область определения и нуль функции x = -7.

На каждом из полученных промежутков определим знак функции F(x) (рис. 3).

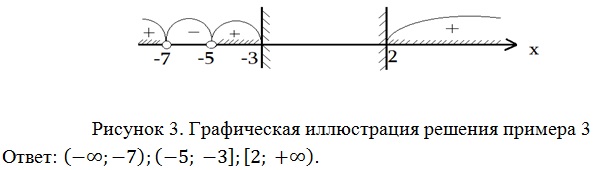
Можно отметить достоинства обобщенного метода интервалов: его простота и универсальность. Этот метод можно эффективно использовать для решения показательных, логарифмических неравенств, а также неравенств смешанного типа. Из недостатков метода – не всегда удобно определять знаки F(x), особенно если нет «хороших» (целых) точек внутри рассматриваемых промежутков.

Список литературы

1. Мордкович, А. Г. Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) [Текст]. / А. Г. Мордкович, П. В. Семенов. – М. : Мнемозина, 2010. – 287 с.
2. Мельников, И. И. Как решать задачи по математике на вступительных экзаменах [Текст]. / И. И. Мельников, И. Н. Сергеев. – М. : Изд-во Моск. ун-та,1990. –303 с.