Электронный научный журнал

Информационно-коммуникационные технологии
в педагогическом образовании

АНАЛИЗ И ПРОЕКТИРОВАНИЕ СИСТЕМЫ ЗАДАНИЙ ФУНКЦИОНАЛЬНОЙ ЛИНИИ НА ИТОГОВОЙ АТТЕСТАЦИИ ПО МАТЕМАТИКЕ В ОСНОВНОЙ ШКОЛЕ

Раздел: Проектирование современных образовательных технологий в системе общего, дополнительного, среднего профессионального и высшего образования

Журнал: Материалы VI Международной очно-заочной научно-практической конференции «Проблемы и перспективы современного образования: практика вуза и школы», Ч. 2

16 марта 2022 г.

Авторы: Позднякова Елена Валерьевна , Малышенко Галина Александровна

Информационно-коммуникационные технологии в педагогическом образовании. http://infed.ru

_______________________________________________________________________

УДК 373.1

Г. А. Малышенко, Научный руководитель: Е. В. Позднякова

G. A. Malyshenko, Scientific supervisor: E. V. Pozdnyakova

Малышенко Галина Александровна, студентка 4 курса ФИМЭ, КГПИ ФГБОУ ВО «КемГУ», г. Новокузнецк, Россия.
Научный руководитель: Позднякова Елена Валерьевна, к. п. н., доцент, КГПИ ФГБОУ ВО «КемГУ», г. Новокузнецк, Россия.

Malyshenko Galina Aleksandrovna, 4th year student, Kuzbass Humanitarian Pedagogical Institute of Kemerovo State University, Novokuznetsk, Russia.
Scientific supervisor: Pozdnyakova Elena Valerievna, candidate of pedagogical Sciences, associate Professor, Kuzbass Humanitarian Pedagogical Institute of Kemerovo State University, Novokuznetsk, Russia.

 

АНАЛИЗ И ПРОЕКТИРОВАНИЕ СИСТЕМЫ ЗАДАНИЙ ФУНКЦИОНАЛЬНОЙ ЛИНИИ НА ИТОГОВОЙ АТТЕСТАЦИИ ПО МАТЕМАТИКЕ В ОСНОВНОЙ ШКОЛЕ

ANALYSIS AND DESIGN OF THE SYSTEM OF TASKS OF THE FUNCTIONAL LINE AT THE FINAL CERTIFICATION IN MATHEMATICS AT THE PRIMARY SCHOOL

 

Аннотация. В статье проведен подробный анализ функциональной линии на итоговой аттестации по математике в форме ОГЭ: элементы содержания функциональной линии, проверяемые образовательные результаты, типы заданий с примерами и типичные ошибки учащихся при их выполнении. Предложена система заданий функциональной линии, позволяющая сформировать не только предметные результаты, но и элементы математической грамотности, представленной в заданиях международных сравнительных исследований PISA.

Annotation. The article provides a detailed analysis of the functional line at the final certification in mathematics in the form of the OGE: the elements of the content of the functional line, the educational results being tested, the types of tasks with examples and typical mistakes of students when performing them. The system of tasks of the functional line is proposed, which makes it possible to form not only subject results, but also elements of mathematical literacy presented in the tasks of international comparative studies PISA.

Ключевые слова: итоговая аттестация по математике, основной государственный экзамен, функциональная линия, система заданий по математике, математическая грамотность.

Keywords: final certification in mathematics, basic state exam, functional line, system of tasks in mathematics, mathematical literacy.

 

Функциональная линия – одна из основных содержательных линий школьного курса математики. Изучение функциональной линии имеет общекультурное значение, способствует всестороннему развитию обучающихся, стимулирует их познавательную активность. С помощью функции описываются многие реальные процессы, что, безусловно, является одним из факторов, повышающих интерес школьников к математике. В курсе алгебры 7-9 классов идёт знакомство с данной линией, школьники узнают, что такое функция, как она задаётся, что называют графиком функции, как его построить и т.д.

При изучении функциональной линии достигаются определённые образовательные результаты. Обучающиеся должны:

  • понимать, что функция – это математическая модель реальных процессов;
  • правильно употреблять функциональную символику и терминологию;
  • находить значение функций, заданных разными способами, решать обратную задачу;
  • находить по графику промежутки монотонности, промежутки знакопостоянства, максимальное и минимальное значения функции;
  • строить графики;
  • интерпретировать графики реальных зависимостей между величинами;
  • знать функции, их графики и свойства:

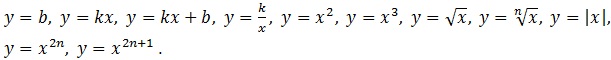
Перечень элементов содержания, относящихся к функциональной линии и проверяемых на основном государственном экзамене по математике (ОГЭ), представлен в таблице 1 [3].

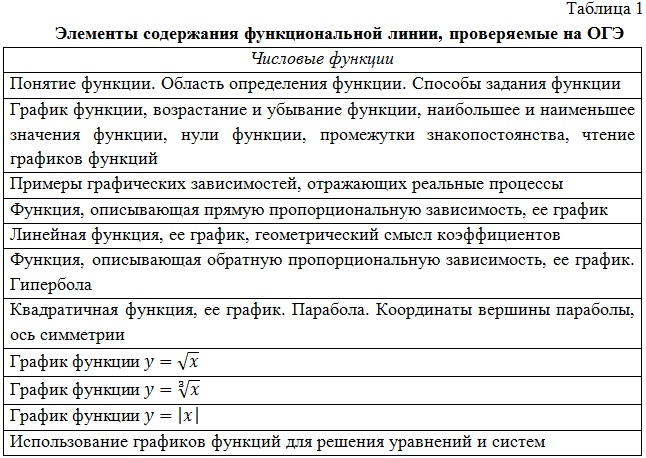
На ОГЭ функциональная линия представлена двумя заданиями:

  1. Задание 11. Относится к первой части и предполагает краткий ответ. За правильное выполнение начисляется 1 балл.
  2. Задание 22. Относится ко второй части, является заданием повышенного уровня сложности, с развернутым ответом.

Рассмотрим типичные ошибки, которые допускают девятиклассники при выполнении заданий функциональной линии.

Так, в решении задания 11, мы наблюдаем: отсутствие знаний по темам функциональной линии (неумение отличить одну функцию от другой, сопоставить функцию с её графиком и т.д.); сложности с растяжением и сдвигами функций.

Типичные ошибки, характерные для задания 22 (задание с развернутым ответом): отсутствие необходимых пояснений; ошибки при преобразовании формул, задающих функции; записано верное значение параметра, но не указано, как оно получено; неправильное построение графика; отсутствуют единичный отрезок на координатных осях, направления координатных осей.

Рассмотрим примеры заданий функциональной линии, представленных на сайте «ОГЭ-2022, Математика: задания, ответы, решения. Обучающая система Дмитрия Гущина» [1]. Для начала обратимся к заданию 11.

  1. Установите соответствие между графиками функций и формулами, которые их задают:
    • графики (рис. 1);
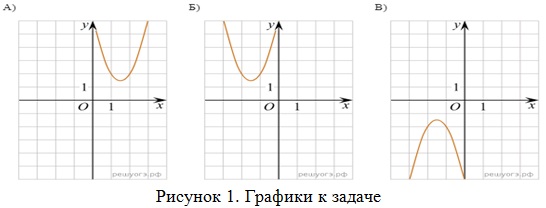
    • формулы:
      1) y = -2x² + 6x - 6;         2) y = -2x² - 6x - 6;         3) y = 2x² + 6x + 6;         4) y = 2x² - 6x + 6.
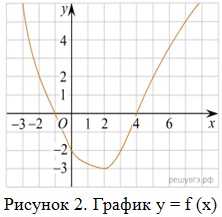
  2. На рисунке 2 изображен график функции y = f (x). Какие из утверждений относительно этой функции неверны? Укажите их номера:

1)   функция возрастает на промежутке [-2; +∞);
2)   f(3) > f(-3); 
3)   f(0) = -2;
4)   прямая у = 2 пересекает график в точках (-2; 2) и (5; 2).

Таким образом, представлены задания на установление соответствия, определения верных утверждений; от ученика требуется умение читать графики функций, сопоставлять график функции и формулу, которая этот график задает.

Рассмотрим пример нестандартного задания функциональной линии с развернутым ответом (задание 22).

1.  Постройте график функции   и определите, при каких значениях m прямая y = m имеет с графиком ровно одну общую точку [1].

Решение:

Раскроем модуль. Для этого сначала определим, при каких значениях x выражение под знаком модуля равно нулю или не существует.

. Следовательно, x = ±3,5, x ≠ 0.

Найдём, на каких промежутках выражение под модулем отрицательно, а на каких положительно (рис. 3).

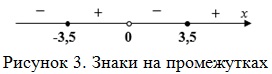
Раскроем модуль и проведём дальнейшие преобразования.

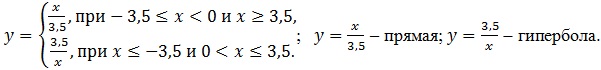
Построим графики полученных функций, учитывая промежутки, на которых они определены (рис. 4).

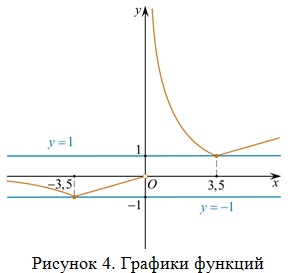
Как видно из построения при m = -1 и m = 1 прямая y = m имеет с графиком ровно одну общую точку, значит m = ±1.

На основе проведенного анализа для успешной подготовки к решению задач ОГЭ функциональной линии предлагаем следующую систему заданий.

Задания на «распознавание» функции по её графику и наоборот.

Например, установите соответствие между графиками функций и формулами, которые их задают (табл. 2).

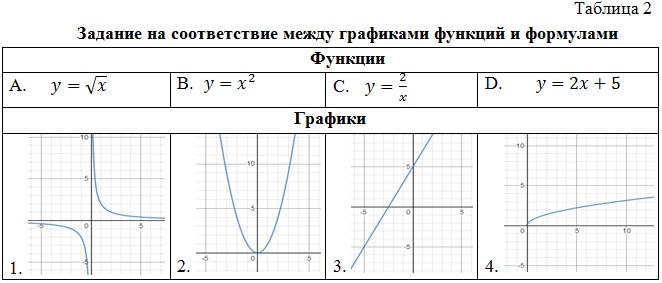
2.  Задания, связанные со сдвигами и растяжениями графиков функций.

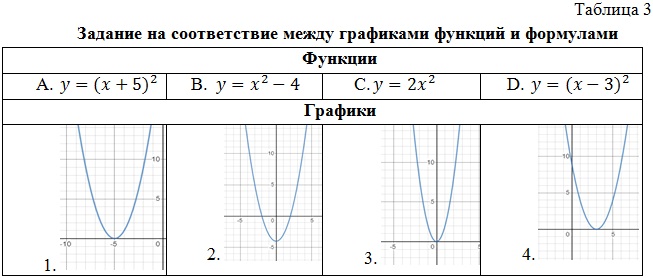
Например, установите соответствие между графиками функций и формулами, которые их задают (табл. 3).

3.  Задания на «чтение» графиков, определение промежутков знакопостоянства, возрастания и убывания функции и т.д.

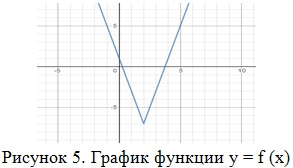
Например, на рисунке 5 изображен график функции y = f (x). Какие из утверждений относительно этой функции неверны? Укажите их номера.

1) Функция возрастает на промежутке [0; 5].
2) f (5) = 5.
3) f (-1) = f (3).
4) y = -7 пересекает график данной функции в двух точках.

4.  Задания на построение простых графиков (со сдвигами и растяжением).

Например, постройте графики следующих функций: .

5.  Задания на построение графиков функций, требующих предварительных преобразований.

Например, постройте графики следующих функций:

6.  Задания с параметром.

Например, используя график функции y = |x² – 2x – 3|, найдите значение а, чтобы прямая у = а имела с графиком функции 3 точки пересечения.

7.  Практико-ориентированные задания.

Считаем целесообразным ввести в систему заданий функциональной линии практико-ориентированные задания, составленные на основе содержания заданий, представленных в международных сравнительных исследованиях по математической грамотности PISA. Рассмотрим пример.

Внутривенные капельные вливания используются для введения жидкости и лекарств пациентам. Для осуществления вливания медсёстрам нужно вычислять скорость падения капель (D), измеряемую в каплях в минуту. Они используют формулу , где k – показатель числа капель в единице объёма, который измеряется в каплях в миллилитре (мл); v – объём вливания, в мл; n – количество часов, в течение которых необходимо делать капельницу.

  1. Медсестра хочет увеличить вдвое время вливания. Приведите точное описание того, как изменится значение D, если n увеличить в два раза, а k и v оставить без изменения.
  2. Медсёстрам также нужно вычислять объём вливания (v), используя скорость падения капель D. Вливание со скоростью 50 капель в минуту необходимо сделать пациенту за 3 часа. Показатель числа капель в единице объёма для данного вливания равен 25 каплям в миллилитре. Каков объём вливания (в мл)? [2]

Можно предложить ученикам самостоятельно составить вопросы к данной задаче, организуя творческую работу в группах.

Таким образом, данная система заданий позволит сформировать не только предметные умения, но и элементы математической грамотности (анализ информации графиков, функциональных зависимостей для понимания истинности или ложности утверждения, решение реальных проблем средствами математики) в области функциональной линии.

Список литературы

  1. ОГЭ-2022, Математика: задания, ответы, решения. Обучающая система Дмитрия Гущина: официальный сайт [Электронный ресурс]. – URL : https://oge.sdamgia.ru/ (дата обращения : 29.01.2022).
  2. Примеры открытых заданий PISA по читательской, математической, естественнонаучной, финансовой грамотности и заданий по совместному решению задач [Электронный ресурс]. – URL : https://school73.minobr63.ru/wp-content/uploads/2021/03/Primery-otkrytyh-zadanij-PISA.pdf (дата обращения : 29.01.2022).
  3. ФГБНУ «Федеральный институт педагогических измерений»: официальный сайт [Электронный ресурс]. – URL : https://fipi.ru/ (дата обращения : 29.01.2022).
PDF