ПРОЕКТИРОВАНИЕ ФАКУЛЬТАТИВНОГО КУРСА «ОРИГИНАЛЬНЫЕ МЕТОДЫ И ПРИЕМЫ РЕШЕНИЯ НЕСТАНДАРТНЫХ ЗАДАЧ ПРИ ПОДГОТОВКЕ К ЕГЭ»

Раздел: Проблемы и перспективы современного физико-математического образования

Журнал: Материалы VII Международной очно-заочной научно-практической конференции «Проблемы и перспективы современного образования: практика вуза и школы», Ч. 1

30 марта 2023 г.

Авторы: Фомина Анжелла Владимировна , Алалыкина Надежда Валерьевна

Информационно-коммуникационные технологии в педагогическом образовании. http://infed.ru

_______________________________________________________________________

УДК 372.851

Н. В. Алалыкина, А. В. Фомина

N. V. Alalykina, A. V. Fomina

Алалыкина Надежда Валерьевна, магистрант 3 курса, КГПИ ФГБОУ ВО «КемГУ», г. Новокузнецк, Россия.
Фомина Анжелла Владимировна, к. ф.-м. н., доцент, декан ФИМЭ, КГПИ ФГБОУ ВО «КемГУ», г. Новокузнецк, Россия.

Alalykina Nadezhda Valeryevna, 3rd year Master's student, Kuzbass Humanitarian Pedagogical Institute of Kemerovo State University, Novokuznetsk, Russia.
Fomina Anzhella Vladimirovna, Candidate of Physical and Mathematical Sciences, Associate Professor, Dean of the Faculty of Informatics, Mathematics and Economics, Kuzbass Humanitarian Pedagogical Institute of Kemerovo State University, Novokuznetsk, Russia.

ПРОЕКТИРОВАНИЕ ФАКУЛЬТАТИВНОГО КУРСА «ОРИГИНАЛЬНЫЕ МЕТОДЫ И ПРИЕМЫ РЕШЕНИЯ НЕСТАНДАРТНЫХ ЗАДАЧ ПРИ ПОДГОТОВКЕ К ЕГЭ»

DESIGN OF THE OPTIONAL COURSE «ORIGINAL METHODS AND TECHNIQUES FOR SOLVING NON-STANDARD PROBLEMS IN PREPARATION FOR THE USE»

Аннотация. В статье рассматриваются нестандартные математические задачи, их роль в школьном курсе математики и при подготовке к единому государственному экзамену. Спроектирован факультативный курс по решению нестандартных задач при подготовке к ЕГЭ. Проведен эксперимент для оценки эффективности факультативного курса.

Annotation. The article discusses non-standard mathematical problems, their role in the school course of mathematics and in preparation for the unified state exam. An optional course was designed to solve non-standard problems in preparation for the exam. An experiment was conducted to evaluate the effectiveness of the optional course.

Ключевые слова: нестандартные задачи, факультативный курс, единый государственный экзамен, эксперимент.

Keywords: non-standard tasks, optional course, unified state exam, experiment.

ЕГЭ одно из испытаний, которое ждет каждого старшеклассника. Обучаясь в старших классах, ученик должен сделать для себя выбор, что он будет сдавать:

ЕГЭ математика базовый уровень, если планирует поступать в гуманитарный вуз;
ЕГЭ математика профильный уровень, если выбор пал на технический вуз.

С каждым годом все меньше выпускников выбирают математику профильного уровня, объясняя это тем, что не справятся. В обществе установилось мнение, что, к сожалению, значительная часть школьников и студентов не способна к усвоению математики.

Одной из основных проблем математического образования является низкая мотивация учащихся к приобретению математических знаний, отсутствие алгоритмического мышления у учащихся, недостаток времени у педагогов для должной подготовки выпускников к сдаче экзамена.

Многие годы дети привыкают решать задания по «накатанному пути» и отступление от привычного алгоритма решения вызывает у них стресс и панику. В этом я убедилась, проходя педагогическую практику. На уроке алгебры в 10 классе было дано задание: найдите первый член и разность арифметической прогрессии [2]. Результаты решения задачи приведены на рисунке 1.

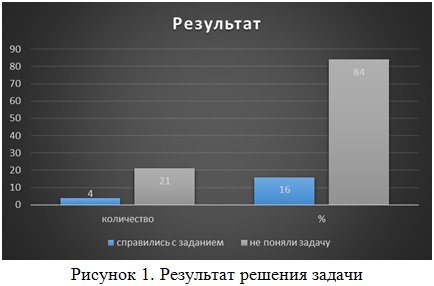
Большинство учеников к 10 классу уже не могут решить задание повышенного или олимпиадного уровня, поэтому при подготовке к экзамену вторая часть заданий ЕГЭ по математике (профиль) вызывает большие трудности.

Анализируя теорию и практику применения нестандартных задач в обучении математике, определим их общую и специфическую роль. Нестандартные задачи:

учат школьников применять не только готовые методы, но и самостоятельно искать новые пути решения задач, т.е. способствуют умению находить необычные способы решения задач;
влияют на развитие сообразительности и смекалки учащихся;
разрушают неверные представления в знаниях и умениях учащихся, предполагают нахождение других связей в знаниях, к переносу знаний в иные условия, к овладению многообразными средствами умственной деятельности;
создают благотворные условия для улучшения прочности и глубины знаний учащихся, обеспечивают осмысленное усвоение математических понятий.

Нестандартные задачи, соответствующие возрасту учащихся:

должны быть понятны и доступны для решения;
не иметь готовых, выученных алгоритмов;
должны быть интересны и содержательны;
для их решения должно быть достаточно тех знаний, которые были усвоены по школьной программе [3, 4].

Очень часто такие задачи встречаются в олимпиадных заданиях, так как дают возможность по-настоящему оценить результаты и способности каждого участника. Нестандартные математические задачи развивают творческое мышление и креативность учащихся [1].

Сложность обучения нестандартным задачам, начиная с десятого класса возрастает. Необходимо приступать к изучению нестандартных задач, встречающихся в ЕГЭ. Одними из самых сложных, но вполне решаемых, нестандартных задач считаются задачи с параметрами и задания, где необходимо применить знания теории чисел.

Задачи экономического содержания, а также задачи оптимизации производства товаров и услуг сравнительно недавно включены во вторую часть ЕГЭ по математике профильного уровня и вызывают значительные затруднения у абсолютного большинства выпускников. В действующих в 10-11 классах учебниках нет материала по решению задач с экономическим содержанием. Для успешного решения подобных задач требуется не только владеть определенным математическим инструментарием, но и уметь строить простейшие математические модели по заданным условиям. За правильное решение задания № 15 на ЕГЭ можно получить два балла.

Задание № 18 в ЕГЭ по математике профильного уровня – свойства чисел. За это задание можно получить 4 балла. Уровень сложности высокий.

Многие учащиеся уверены, что с этим заданием справится только гений. Но если повторить ряд тем из курса математики, начиная с 6 класса, то задание станет доступным многим ученикам. К сожалению, эту задачу не получится решить, подобрав типовой алгоритм. Тут придется поразмышлять.

Задачи на делимость в ЕГЭ – это задачи олимпиадного типа, нестандартные задачи. Данные задачи можно разделить на несколько типов:

числовые наборы на карточках и досках;
последовательности и прогрессии;
сюжетные задачи;
разные задачи на числа.

Это и многое другое наталкивает на мысль о проектирование факультативного курса. Введение в школе курса по выбору приводит к разделению учебного материала на основной, обязательный для всех учащихся, и дополнительный, рассчитанный на удовлетворение повышенных интересов отдельных учеников. Что дает возможность повысить уровень общего образования, не допуская перегрузки ребят обязательными учебными предметами.

Курс «Оригинальные методы и приемы решения нестандартных задач при подготовке к ЕГЭ» рассчитан на 34 часа, которые проводятся в течение года обучения с учащимися 10-го класса.

В курсе решается большое количество нестандартных задач, поэтому появляется возможность обучению учащихся моделированию процесса решения математических задач. Акцент в проведении курса делается в сторону «абитуриентской» математики (подготовке к ЕГЭ).

Факультативный курс состоит из двух блоков:

Финансовая математика (№ 15, профиль).
Числа и их свойства (№ 18, профиль).

Наблюдения за ходом внедрения факультативного курса, полученные результаты давали возможность для уточнения, улучшения содержания и методических рекомендаций по его использованию.

Во время проведения занятий было выявлено, что ученики усвоили тему из школьного курса алгебры и имеют представление о том, что такое нестандартные задачи. Но при выполнении предложенных заданий у учащихся возникали затруднения, так как задачи требовали исследовательских навыков, логического мышления, что, как оказалось, у них развито слабо.

Это говорит о том, что школьный курс ограничен и не позволяет рассматривать задачи, требующие не только действий по алгоритму.

Самостоятельный поиск решения оказался для учеников сложным, но все же позволил школьникам проявить свои способности, заставил задуматься над задачами. У некоторых учеников есть склонность к изучению математики, но базовый курс математики не создает условий для подтверждения выбранной траектории обучения в соответствии со склонностями, способностями и потребностями школьника и развития этих способностей.

Чтобы оценить эффективность курса ученикам были даны задания из пробного ЕГЭ математика (профиль) 2023 г.

31 декабря 2016 года Василий взял в банке 5 460 000 рублей в кредит под 20 % годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 20 %), затем Василий переводит в банк x рублей. Какой должна быть сумма x, чтобы Василий выплатил долг тремя равными платежами (то есть за три года)? (задание № 15) [5].
Дано трёхзначное натуральное число (число не может начинаться с нуля).
а) Может ли частное этого числа и суммы его цифр быть равным 12?
б) Может ли частное этого числа и суммы его цифр быть равным 87?
в) Какое наименьшее натуральное значение может иметь частное данного числа и суммы его цифр? (задание № 18) [5].

Результат отражен на рисунке 2 «Результат эксперимента».

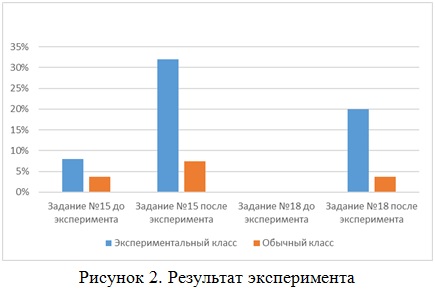
На основе полученных данных формирующего эксперимента можно сделать выводы:

Предлагаемый факультативный курс может быть использован при подготовке учащихся к ЕГЭ.
Дифференцированный подход к учащимся позволил повысить интенсивность их деятельности и добиться на различных этапах однородных результатов.
Результаты проведённого исследования указывают на эффективность предлагаемого факультативного курса.

Список литературы

Алалыкина, Н. В. Нестандартные математические задачи как способ формирования и развития творческого мышления и креативности обучающихся профильных классов [Текст]. / Н. В. Алалыкина, А. В. Фомина // Современная школа России. Вопросы модернизации, № 6 (37) сентябрь, 2021 : Материалы международного научного журнала, 2021. – Москва. – С. 48-51.
Алгебра. 9 класс [Текст] : учебник для учащихся общеобразовательных организаций / А. Г. Мерзляк, В. Б. Полонский, М. С. Якир. – М., 2020. – 318 с.
Колягин, Ю. М. Учебные математические задачи творческого характера [Текст]. / Ю. М. Колягин // Роль и место задач в обучении математике, 1973. – М. – Вып. 2. – С. 5-19.
Кордемский, Б. А. Очерки о математических задачах на смекалку [Текст]. / Б. А. Кордемский. – М. : Учпедгиз, 1958. – 116 с.
ФГБНУ «Федеральный институт педагогических измерений» : сайт [Электронный ресурс]. – URL : https://fipi.ru/ege/otkrytyy-bank-zadaniy-ege (дата обращения : 29.01.2023).

PDF