ИЗУЧЕНИЕ РЕКУРСИВНЫХ АЛГОРИТМОВ В СРЕДЕ ООП LAZARUS И GAMBAS В ДИСЦИПЛИНЕ «ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ НА ЭВМ»
Раздел: Научно-методическое обеспечение подготовки по направлению "Педагогическое образование" //Тематический сборник научных трудов кафедры Теории и методики преподавания информатики
Журнал: Сборник научных трудов кафедры ТиМПИ
15 августа 2015 г.
Авторы: Буяковская Ирина Александровна
И. А. Буяковская
ИЗУЧЕНИЕ РЕКУРСИВНЫХ АЛГОРИТМОВ В СРЕДЕ ООП LAZARUS И GAMBAS В ДИСЦИПЛИНЕ «ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ НА ЭВМ»
Дисциплина «Практикум по решению задач на ЭВМ» входит в вариативную часть профессионального цикла программы бакалавриата по направлению «Педагогическое образование» профиль «Информатика» с кодом (Б.3.В) и изучается на 4 курсе в 7,8 семестрах. В рамках данной дисциплины предусматривается решение задач в средах объектно-ориентированного программирования Lazarus или Gambas.
Выбор данного программного обеспечения обусловлен переходом образовательных учреждений на свободное программное обеспечение и операционную среду Linux, что способствовало изменениям в системе подготовки будущих учителей информатики, ориентированную на применение бесплатных программных сред. Среда Gambas основана на языке Basic и аналогична проприетарному программному продукту Microsoft Visual Basic, среда Lazarus является свободной средой разработки программного обеспечения для компилятора Free Pascal. В настоящее время Basic и Pascal - это наиболее популярные языки, применяемые для обучения программированию в образовательных учреждениях, так как Единый государственный экзамен по дисциплине "Информатика и информационно-коммуникационные технологии" включает темы, касающиеся программирования, на примере данных языков программирования.
В рамках дисциплины «Практикум по решению задач на ЭВМ» обучающиеся закрепляют знания, связанные с реализацией типовых алгоритмов и структур данных в объектно-ориентированных средах программирования, полученных в рамках дисциплин «Математическая логика и теория алгоритмов» «Программирование». Поэтому данный курс включает аудиторную работу, представленную только лабораторными занятиями на которых рассматриваются такие темы как: массивы, строки, файлы, записи, графика и рекурсия.
Рассмотрим на примере темы «Рекурсия» какими заданиями представлена фронтальная и индивидуальная работа студентов.
Перед решением типовой задачи необходимо актуализировать знания по данной теме, полученные в рамках других дисциплин и связанных с опорными понятиями: рекурсия, глубина рекурсии, процедура, функция, формальные и фактические параметры, глобальные и локальные переменные.
Рекурсивные алгоритмы на графике представлены несколькими вариантами задач, связанными с повторением графического примитива с уменьшением размера, а также с его смещением как относительно оси ординат, так и оси абсцисс. Необходимо обратить внимание на тот факт, что рекурсивные алгоритмы наиболее показательны на графике, но они также применимы и задачах вычислительного характера.
В качестве примера в данном случае можно привести функцию вычисления факториала:
Function Factorial (N: integer): integer;
Begin
If N=1 then Factorial:=1
Else Factorial:=N*Factorial(N-1)
End;
Здесь Factorial (N) определяется через значение Factorial (N-1), которое определяется через Factorial (N - 2), и т.д. до сведения к значению Factorial (0), которое определено явно и равно 1.
Любое рекурсивное описание должно содержать явное определение для некоторых значений аргумента (или аргументов), так как иначе процесс сведения оказался бы бесконечным. Таким образом, при рекурсивном описании необходимо наличие базовой части описания, которая обеспечивала бы завершение рекурсивных вызовов функции (процедуры).
Использование рекурсивных процедур и функций делает программу в целом более гибкой и наглядной, но не всегда эффективной, так как работает такая программа, как правило, медленнее и требуют больше памяти. Дело в том, что при каждом вызове рекурсивной процедуры или функции отводится память под локальные переменные.
Представим примеры фронтальных лабораторных задач на применение рекурсии на графике в среде Lazarus и Gambas.
Задача 1. Выполните рекурсивное построение графического примитива, как показано на рисунке 1 в среде Lazarus. Для этого на форме расположим кнопку Button1, по нажатию на которую будет производиться рекурсивное построение, Edit1 для задания глубины рекурсии (количество построений), Panel1для рисования изображения согласно условию задачи.
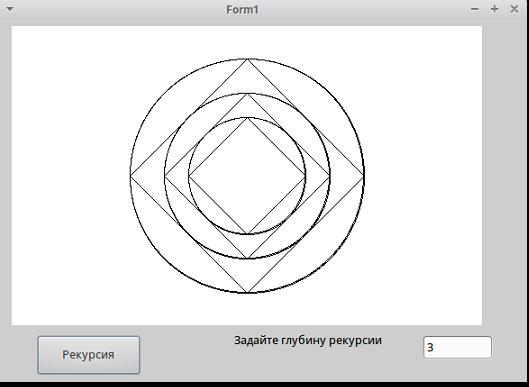
Рис. 1. Рекурсивное построение ромба, вписанного в окружность
Ниже представлен листинг к задаче №1.
Листинг 1. Рекурсивное построение ромба, вписанного в окружность.
unit Unit1;
{$mode objfpc}{$H+}
interface
uses
Classes, SysUtils, FileUtil, Forms, Controls, Graphics, Dialogs, ExtCtrls,
StdCtrls;
type
{ TForm1 }
TForm1 = class(TForm)
Button1: TButton;
Edit1: TEdit;
Label1: TLabel;
Panel1: TPanel;
procedure Button1Click(Sender: TObject);
procedure Figura(n,r: Integer);
private
{ private declarations }
public
{ public declarations }
end;
var
Form1: TForm1;
x,y:integer;
implementation
{$R *.lfm}
procedure TForm1.Figura(n,r: Integer);
begin
Panel1.Canvas.EllipseC(x,y,r,r);
Panel1.Canvas.Line(x,y-r,x+r,y);
Panel1.Canvas.Line(x+r,y,x,y+r);
Panel1.Canvas.Line(x,y+r,x-r,y);
Panel1.Canvas.Line(x-r,y,x,y-r);
if n>1 then Figura(n-1,round(r*sqrt(2)/2));
end;
procedure TForm1.Button1Click(Sender: TObject);
var n:integer;
begin
x:= Panel1.Width div 2;
y:= Panel1.Height div 2;
n:=StrToInt(Edit1.Text);
Panel1.Canvas.FillRect(Rect(0,0,Panel1.Width,Panel1.Height ));
Figura(n,x div 2);
end;
end.
Задача 2. Выполните рекурсивное построение графического примитива, как показано на рисунке 2 в среде Gambas. В данной задаче необходимо на форме разместить DrawingArea , и две кнопки Button. Далее добавляем TextBox для ввода количества окружностей и метку label. В данной задаче при рисовании окружности используется метод DrawCircle(x,y,r), а для воспроизведения окружности по четырем направлениям, необходимо организовать четыре вызова пользовательской процедуры.
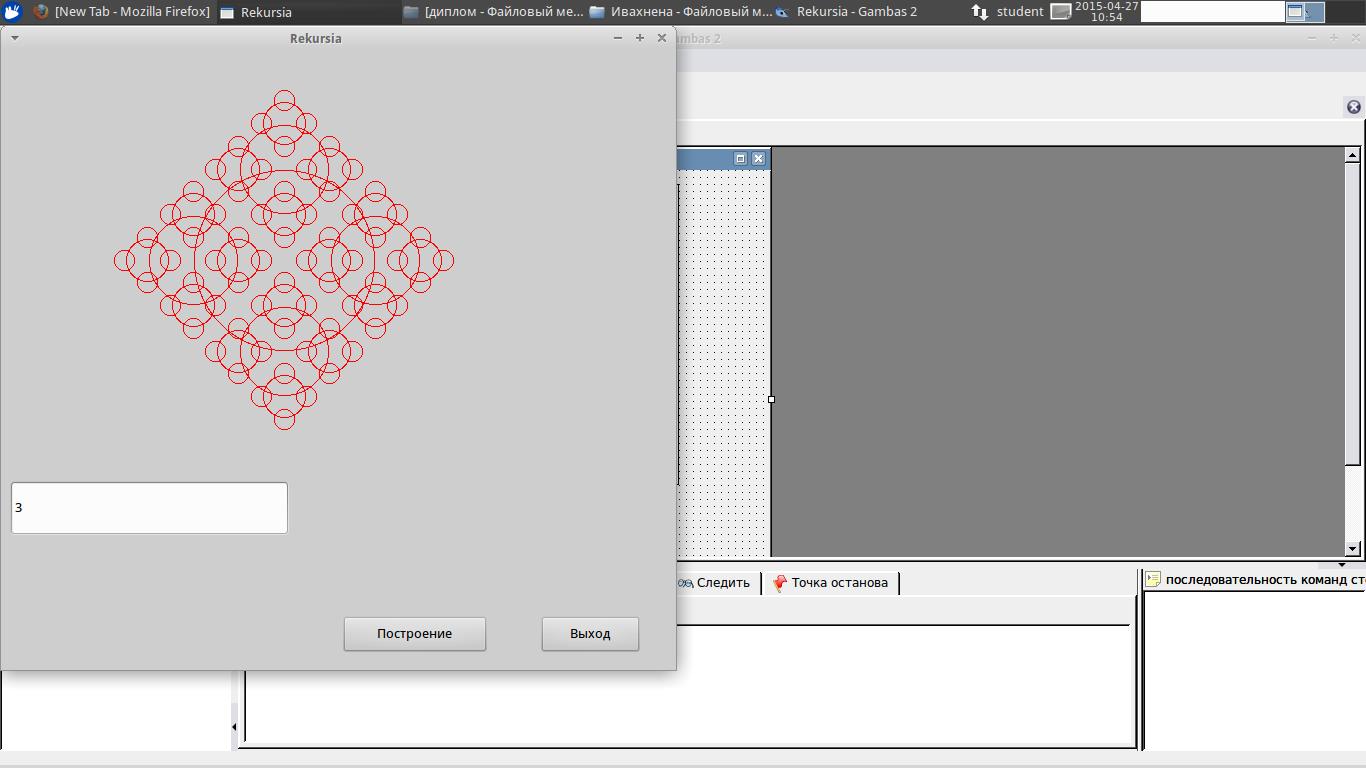
Рисунок 2. Рекурсивное построение окружностей
Ниже представлен листинг к задаче № 2.
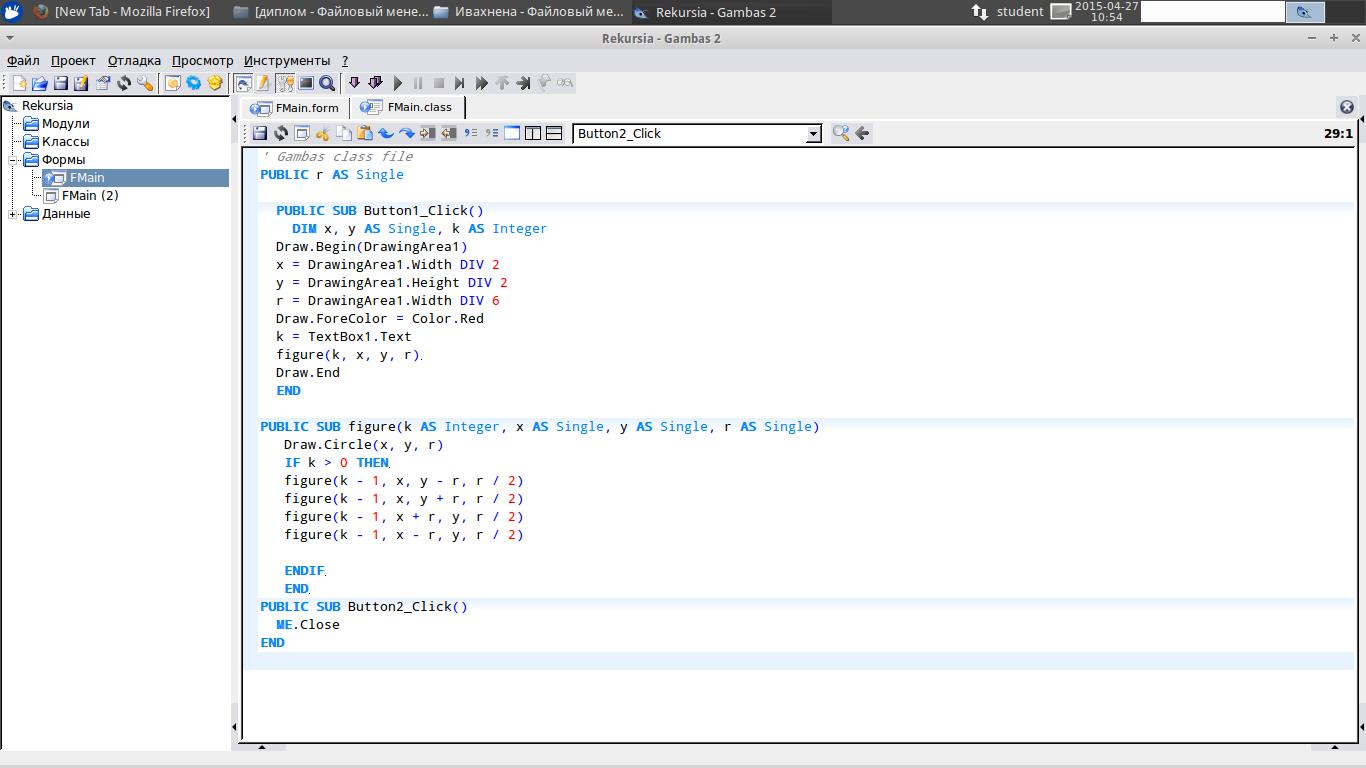
Рисунок 3. Листинг рекурсивного построения окружностей
В приведенных примерах остановка рекурсивного построения осуществляется на основе заданной пользователем глубины рекурсии, введенной в однострочное текстовое поле. Другой вариант задания данной величины: использование простого диалогового окна InputBox. Рекурсивный алгоритм можно останавливать в зависимости от размера графического примитива, который уменьшается с каждым построением фигуры.
После решения фронтальных задач, студентам предлагаются индивидуальные задания, примеры которых приведены в учебном пособии «Введение в структурное программирование» [1] приведем несколько примеров:
1. Написать программу, выводящую в графическом режиме следующее рекурсивное построение, в основании которого лежит квадрат:
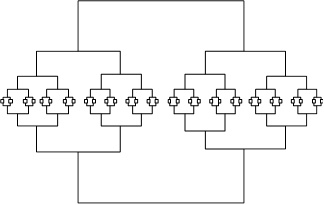
2. Написать программу, выводящую в графическом режиме следующее рекурсивное построение, в основании которого лежит квадрат:
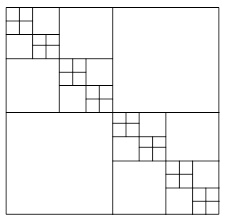
Результат оценивается в зависимости от правильности выполнения индивидуального задания. Весьма важным в данном случае является временной фактор. Студент должен справляться с решением индивидуальной задачи по теме в рамках лабораторного занятия.
Список литературы
1. Можаров М.С., Бойченко Г.Н. Введение в структурное программирование: (Учебное пособие. Рекомендовано Учебно-методическим объединением по образованию в области прикладной информатики в качестве учебного пособия для студентов высших учебных заведений, обучающихся по специальности 080801 «Прикладная ин-форматика (в юриспруденции)» и другим экономическим специ-альностям)//Новокузнецк: КузГПА, 2009. -Ч.1 - 2. - 238 с.
2. Можаров М.С., Коткин С.Д. О развитии содержательной линии «моделирование и формализация» в школьном курсе «информатика и икт»//Информатика и образование. 2010. № 4. С. 95-99.
3. Можаров М.С. Структурное программирование в примерах и решениях// Учебное пособие. Рекомендовано УМО ГОУ ВПО РГПУ им. А.И.Герцена» в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлению 050200 Физико-математическое образование (Регистрационный номер рецензии №782 от 07.04.2010г.) / Новокузнецк, 2010.
4. Можаров М.С., Журавлёв С.В. Некоторые особенности преподавания программирования за рубежом //Актуальные вопросы современной науки. 2015. № 40. С. 122-132.
5. Можаров М.С. Формирование профессиональной мобильности будущего учителя информатики // Педагогическая информатика. 2009. № 3. С. 31-37.
