ОБУЧЕНИЕ СТУДЕНТОВ ВЫПОЛНЕНИЮ БАЗИСНЫХ ФИНАНСОВЫХ РАСЧЕТОВ НА КОМПЬЮТЕРЕ
Раздел: Научно-методическое обеспечение подготовки по направлению «Прикладная информатика в образовании» // Тематический сборник научных трудов кафедры Теории и методики преподавания информатики
Журнал: Сборник научных трудов кафедры ТиМПИ
14 октября 2015 г.
Авторы: Дробахина Анастасия Николаевна
А. Н. Дробахина
ОБУЧЕНИЕ СТУДЕНТОВ ВЫПОЛНЕНИЮ БАЗИСНЫХ ФИНАНСОВЫХ РАСЧЕТОВ НА КОМПЬЮТЕРЕ
Базисные финансовые вычисления - вычисления, определяющие величину финансовых потоков выплат и процентов по вкладам, ссудам, для определения доходности, текущей и конечной стоимости ценных бумаг.
Предоставление денег в долг во временное пользование может осуществляться различными способами: в виде денежной ссуды, сберегательного счета, открытия депозита, покупки облигаций и векселей и т.д. На занятые деньги с должника начисляются проценты.
В качестве единицы периода времени в финансовых расчетах, как правило, принят год, однако возможно использование и других периодов: полугодие, квартал, месяц, день.
Начисление процентов по простой процентной ставке
Сущность простых процентов в том, что они начисляются на одну и ту же величину капитала в течение всего срока ссуды.
Расчет простых процентов может быть произведен одним из трех способов:
1. Обыкновенные проценты с приближенным числом дней ссуды, или, как часто называют, «германская практика расчета», когда продолжительность года условно принимается за 360 дней, а целого месяца - за 30 дней. Этот способ обычно используется в Германии, Дании, Швеции.
2. Обыкновенные проценты с точным числом дней ссуды, или «французская практика расчета», когда продолжительность года условно принимается за 360 дней, а продолжительность ссуды рассчитывается точно по календарю. Этот способ имеет распространение во Франции, Бельгии, Испании, Швейцарии.
3. Точные проценты с точным числом дней ссуды, или «английская практика расчета», когда продолжительность года и продолжительность ссуды берутся точно по календарю. Этот способ применяется в Португалии, Англии, США.
Начисление процентов по постоянной простой процентной ставке
Для ссуд со сроком меньше года для начисления выплат и процентов обычно используется простая процентная ставка:
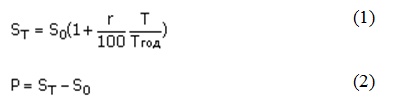
Где:
SО - первоначальный размер ссуды;
SТ - размер выплат по окончании ссуды;
P - проценты на ссуду;
T - срок ссуды в днях;
T ГОД - временная база (число дней в году);
r - годовая процентная ставка;
Временная база обычно задается равной 360 или 365 дням, дата выдачи и дата погашения считаются за один день.
Задание 1. Ссуда в размере 50 тыс. руб. выдана на 2 месяца под 25 % годовых. Определить размер выплат по окончании ссуды и проценты на ссуду при использовании английской практики расчета.
- Итак, по условию задачи S0=50 000; T =61; Tгод= 365; r = 25;
- Запишем условие задачи следующим образом:
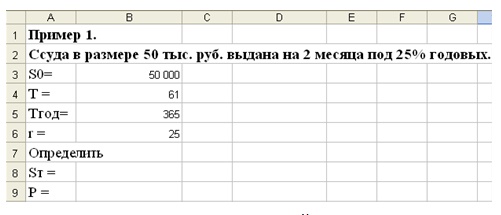
Рисунок 1. Определение наращенной суммы вклада по простой процентной ставке
- В ячейке В8 запишем формулу для подсчета размера выплат по окончании ссуды, подставив в формулу (1) адреса ячеек с данными (из диапазона В3:В6). Получим значение 52 089 руб.
- Аналогично, в ячейке В9 запишем формулу для подсчета процентов и получим значение 2089 руб.
Начисление процентов по постоянной сложной процентной ставке
Сложные процентные ставки обычно используются для долгосрочных ссуд со сроком более года. При сложной процентной ставке процентный платеж в каждом расчетном периоде добавляется к капиталу предыдущего периода, а процентный платеж в последующем периоде начисляется уже на эту наращенную величину первоначального капитала.
Для начисления выплат по постоянной сложной процентной ставке обычно используется формула:

Задание 2. Гражданин желает поместить 100000 руб. на 5 лет под сложную ставку в 15% годовых. Определить размер вклада по окончании срока.
В ячейке В8 запишем формулу для подсчета срока вклада в днях, а в ячейке В9 - формулу для подсчета размера вклада. Представим условие задачи и ее решение на рабочем листе следующим образом:

Рисунок 2. Определение наращенной суммы вклада по сложной процентной ставке
Получим, что к концу срока размер вклада составит 201 136 руб.
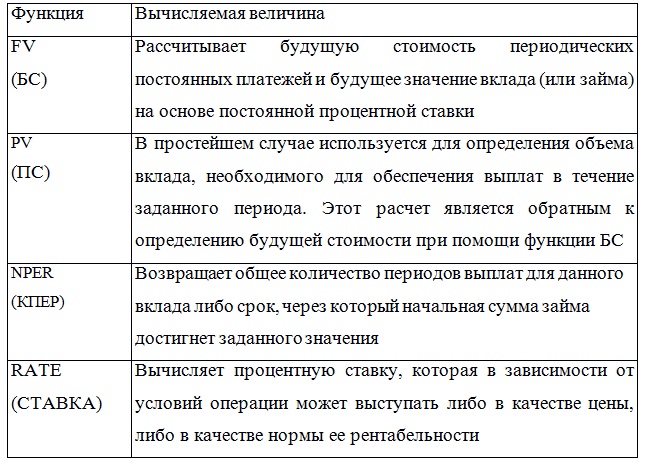
В таблице 1 представлен список некоторых функций, которые могут быть использованы при выполнении расчетов при использовании постоянной процентной ставки.
Таблица 1. Встроенные финансовые функции
При задании аргументов перечисленных функций важно соблюдать правило: если некоторые суммы денег являются платежами (расходами), то соответствующие аргументы должны указываться со знаком минус. Знак минус можно указывать как в ячейках с данными, так и в формуле перед соответствующими аргументами.
Если значением формулы является величина платежа, то это значение выдается также со знаком минус. На мониторе в этом случае и число, и знак минус перед ним выделяются красным цветом.
Кроме того, при работе в электронных таблицах с финансовыми функциями необходимо учитывать специфику задания значения аргументов:
- можно вводить как сами значения аргументов, так и ссылки на адреса ячеек, их содержащих;
- все расходы денежных средств (платежи) представляются отрицательными числами, а все поступления денежных средств - положительными числами;
- процентная ставка вводится с использованием знака % или в процентном формате;
- все даты как аргументы функций имеют числовой формат.
Рассмотрим примеры использования перечисленных функций для решения конкретных задач.
Задание 3. Гражданин делает накопления, вкладывая ежемесячно 1000 руб. в банк, выплачивающий 12 % годовых. Какая сумма будет на счету через 3 года?
Решение. Будем использовать встроенную функцию FV. Чтобы узнать количество выплат, умножим количество лет кредита на 12. Чтобы получить месячную процентную ставку, разделим годовую ставку на 12.
Решение задачи и полученный ответ представлены на рисунке ниже.

Рисунок 3. Применение встроенных функций
Задание 4. Фирма посылает служащих на учебу и желает положить в банк, который выплачивает 10% сложных годовых, такую сумму, чтобы иметь возможность снимать с этого счета ежегодно по 10 000 руб. для выплаты стипендии. Вклад должен быть исчерпан к концу пятилетнего срока учебы (деньги снимаются в конце каждого года). Какую сумму фирма должна положить в банк?
Запишем условие задачи следующим образом:
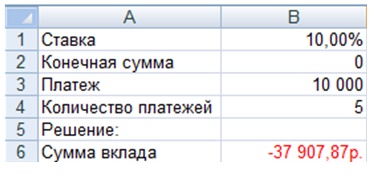
Рисунок 4. Применение встроенных функций
Для решения данной задачи необходимо воспользоваться функцией PV (ПС). Ответ: 37 907,87руб.
Тренинг
Задания, представленные ниже, решить, используя изученные формулы и функции. Полученные ответы округлить до целых.
1. На депозит вложено 90 тыс. руб. сроком на 181 день. Процентная ставка 15% годовых. Какая сумма будет на счете к концу срока, если начисление процентов производится по схеме простых процентов. Временная база 360 дней.
2. На депозит вложено 70 тыс. руб. сроком на 2 года. Процентная ставка 7% годовых. Какая сумма будет на счете к концу срока, если начисление процентов производится по схеме сложных процентов. Временная база 365 дней.
3. Рассчитать, какая сумма окажется на счете, если 27 тыс. рублей положены на 33 года под 13,5% годовых. Проценты начисляются каждые полгода.
4. Предположим, Вы хотите зарезервировать деньги для специального проекта, который будет осуществлен через год. Вы собираетесь вложить 1 млн. рублей под 60% годовых. Вы собираетесь также вкладывать по 100 тыс. рублей в начале каждого месяца в течение 12 месяцев. Сколько денег будет на счете в конце 12 месяцев? (БС, 3467654,6)
5. Есть два варианта инвестирования средств в течение 4 лет: а) в начале каждого года под 26% годовых; б) в конце каждого года под 38% годовых. Пусть ежегодно вносится 300 тыс. рублей. Определить, сколько денег окажется на счете в конце четвертого года для каждого варианта.
Использованная литература
1. Дробахина А.Н. Использование возможностей табличного процессора Excel для расчетов по сложным процентным ставкам / А.Н. Дробахина // Информатика и образование. - № 12. - 2008. - С. 50 - 54.
2. Новиков А.М Финансовые и коммерческие расчеты: Учебное пособие/ А.М. Новиков - М.: РАГС, 2010. - 138 с.
3. Четыркин Е.М. Методы финансовых и коммерческих расчетов. / Е.М. Четыркин - М.: Дело Лтд, 1995. - 195 с.
