ОРГАНИЗАЦИЯ НАУЧНО-ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЫ ШКОЛЬНИКОВ ПО ПРОГРАММИРОВАНИЮ ПО ТЕМЕ «РАЗРАБОТКА СТЕКОВОГО КАЛЬКУЛЯТОРА»
Раздел: Материалы I Всероссийской очно-заочной практической конференции "Математика, физика, информатика:проблемы и перспективы современного образования" (Новокузнецк, февраль 2016)
Журнал: Проблемы и перспективы современного образования в области информатики и ИКТ
11 мая 2016 г.
Авторы: Можаров Максим Сергеевич , Арзамасцева Н. А.
М. С. Можаров, Н. А. Арзамасцева
ОРГАНИЗАЦИЯ НАУЧНО-ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЫ ШКОЛЬНИКОВ ПО ПРОГРАММИРОВАНИЮ ПО ТЕМЕ «РАЗРАБОТКА СТЕКОВОГО КАЛЬКУЛЯТОРА»
Российский опыт организации исследовательской работы школьников по решению задач повышенной сложности по программированию показывает, что подбор заданий для таких занятий — это значимая методическая задача учителя информатики.
В условиях ограниченного времени занятий, а также высокой сложности решаемых задач учитель вынужден рассматривать только такие условия задач, которые максимально раскрывают не только методы и технологии программирования, но и такие важные аспекты, связанные с этими технологиями, как структуры организации данных.
Кроме того, наибольший интерес представляют задания, позволяющие организовать работу школьников в проектном режиме, задействовать максимальное количество компетенций.
Одной из таких задач является задача разработки стекового калькулятора.
Действительно, решая эту задачу, школьник проводит самостоятельное исследование: понятие стека, алгоритмы работы со стеком, анализ алгебраических выражений, инфиксная запись, постфиксная запись и префиксная запись выражений.
После исследования проблемной области школьнику необходимо применить найденный самостоятельно материал, связать ключевые структуры данных и алгоритмы. А в итоге создать программный продукт «Калькулятор», позволяющий обеспечить результативность процесса обучения.
В качестве освоения содержания занятий по этой теме школьники знакомятся с исторической справкой, ключевыми определениями и программными решениями. Приведем фрагменты учебных материалов для организации занятия.
Работа со стеком
Стек (с англ. Stack-стопка) — это абстрактный тип данных, который представляет собой список элементов, составленных по принципу LIFO. Обычно принцип работы стека сопоставляют со стопкой полотенец: чтобы взять второе сверху, нужно снять верхнее. Понятие стека было введено Аланом Матисоном Тьюрингом в 1946. А в 1957 году немецкие ученые Клаус Самельсон и Фридрих Бауэр запатентовали данную идею.
Во многих языках стеком можно назвать любой список, так как им доступны операции pop и push. В языке C++ стандартная библиотека имеет класс с реализованной структурой и методами.
Со стеком можно выполнить три операции: присоединение элемента (иначе проталкивание, push), исключение элемента (pop) и чтение головного элемента (peek).
Для проталкивания (push) выбирается новый элемент, указывающий на предыдущий. Головным теперь становится новый элемент.
При удалении убирается первый элемент, а головным становится тот, на который был указатель у этого объекта (следующий элемент).
Одно из самых главных применений стека - вызов подпрограмм. На стеке сохраняется адрес возврата после завершения подпрограммы. При каждом вложенном (в т.ч. при рекурсивном) вызове подпрограмм на стек добавляются новые адреса возврата. В каждой операции возврата из подпрограммы (return) управление передается по стеку и с него снимается адрес возврата. Это применение является очень важным для программирования в большинстве процессоров стек возврата реализован аппаратно в системе команд, но в остальных случаях стек моделируется на более общих структурных данных.
Самые распространенные в программировании два принципа реализации стека: на базе связанного списка и на базе массива. В первом случае для каждого элемента стека задается блок памяти, достаточный для хранения значений и ссылок на предыдущий и следующий элементы стека. Во втором случае для хранения значений предлагается сплошной массив ячеек, которые используются по мере необходимости. Реализация на базе массива проще, эффективнее и экономичнее по расходу памяти, но для нее требуется заранее знать предельный размер стека, и она может привести к трудно выявляемым ошибкам. Реализация на базе списков более надежна, но менее эффективна.
Постфиксная и инфиксная нотации
С древности в математике существовала традиция записывать операцию между аргументами вида (х+у). Такая форма записи называется инфиксной. Форма вида (ху+)называется постфиксной, в ней оператор стоит после аргументов. Также ее называют обратной польской записью, в честь польского логика Я. Лукасевича, который изучал свойства такой записи.
Обратная польская нотация (ОПН) — это форма записи математических и логических предикатов, в которой оператор стоит после аргументов. ОПН была разработана австралийским специалистом по теории вычислительных машин Чарльзом Хэмблином в 50-х годах на основе польской нотации, которая была предоставлена в 1920 г. математиком Яном Лукасевичем из Польши. Данная работа была представлена на конференции в июне 1957г., и издана в 1957 и 1962гг.
Обратная польская запись имеет несколько преимуществ при записи алгебраических формул. Во-первых, любая формула может быть записана без скобок. Во-вторых, она удобна для вычисления в машинах со стеками. В-третьих, инфиксные операторы имеют приоритеты, которые произвольны и нежелательны.
Отличительной особенностью постфиксной записи является то, что все аргументы стоят перед знаком оператора. В общем виде запись выглядит так:
- Запись набора операций состоит из последовательности аргументов и знаков операций. Аргументы в предложении разделяются пробелами.
- Предложение читается слева направо. Операции выполняются в том порядке, в котором они записаны.
- Результатом вычисления выражения становится результат последней вычисленной операции.
Особенности обратной польской записи следующие:
Порядок выполнения операторов определяется порядком следования знаков операторов в предложении однозначно, поэтому нет необходимости использовать скобки или вводить приоритеты.
В отличие от инфиксной записи, невозможно использовать одни и те же знаки для записи унарных и бинарных операций. Так, в инфиксной записи в выражении 6 * (-4 + 9) используется знак «минус» как символ унарной операции (изменение знака числа), а в выражении (11 - 16) * 4 применяется такой же знак для обозначения бинарной операции (вычитания). Конкретная операция определяется тем, в какой позиции находится знак. Постфиксная запись не позволяет этого: запись 6 4 - 9 + * (постфиксная запись первого выражения) будет прочитана как ошибочная, так как невозможно определить, что «минус» после 6 и 4 обозначает не вычитание; в результате будет сделана попытка вычислить сначала 6 - 4, затем 2 + 9, после этого выяснится, что для операции умножения не хватит аргументов. Чтобы всё же записать это выражение, придётся либо переформулировать его, либо ввести для операции изменения знака отдельное обозначение, например, «±»: 6 4 ± 9 + *.
Так же, как и в инфиксной записи, в ОПН одно и то же вычисление может быть записано в различных вариантах. Например, выражение (11 - 16) * 4 в ОПН можно записать как 11 16 - 4 *, а можно — как 4 11 16 - *.
Из-за отсутствия скобок постфиксная запись короче инфиксной. Поэтому при вычислении на калькуляторах увеличивается скорость работы оператора (уменьшается количество нажимаемых клавиш), а в программируемых устройствах сокращается объём тех частей программы, которые описывают вычисления. Это немаловажно для портативных и встроенных вычислительных устройств, имеющих жёсткие ограничения на объём памяти.
После знакомства школьников с теоретическим материалам переходят к разработке алгоритмов.
На первом этапе школьникам предлагается разработать алгоритм для вычисления значения выражения в постфиксной форме. Для его реализации необходимо применить операции работы со стеком и реализовать его в виде одномерного массива и библиотеки подпрограмм. Этот алгоритм достаточно прост и наглядно демонстрирует необходимость использования постфиксной формы.
На рисунке 1 приведена блок-схема не детализованного алгоритма.
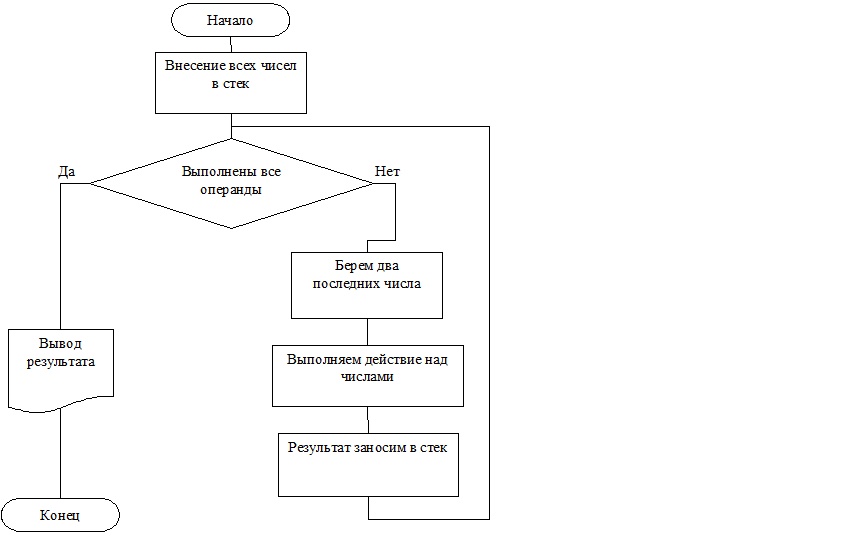
Рисунок 1. Блок-схема алгоритма для вычисления значения выражения в постфиксной форме
Однако реализация этого достаточно простого алгоритма требует разработки следующих подпрограмм: 1) Calculate – функция принимает выражение, проверяет и выводит результат; 2) GetExpr – функция преобразует входную строку в постфиксную запись; 3) Counting – функция вычисляет выражение из постфиксной записи; 4) IsDelimiter – функция определяет разделитель; 5) IsOpperator – функция определяет оператор; 6) GetPriority – функция возвращает приоритет.
Приведем алгоритмы вспомогательных функций, которые школьники разрабатывают на втором этапе (Рисунок 2, Рисунок 3, Рисунок 4).
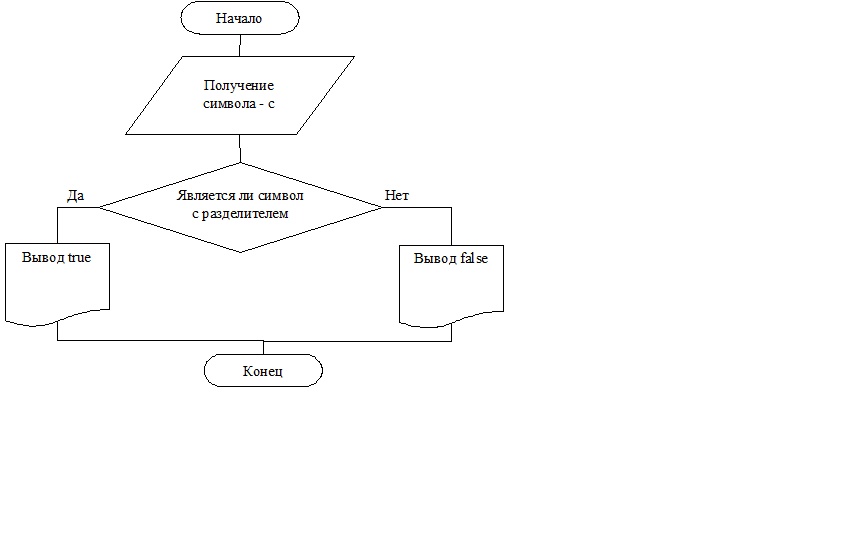
Рисунок 2. Блок-схема алгоритма IsDelimiter
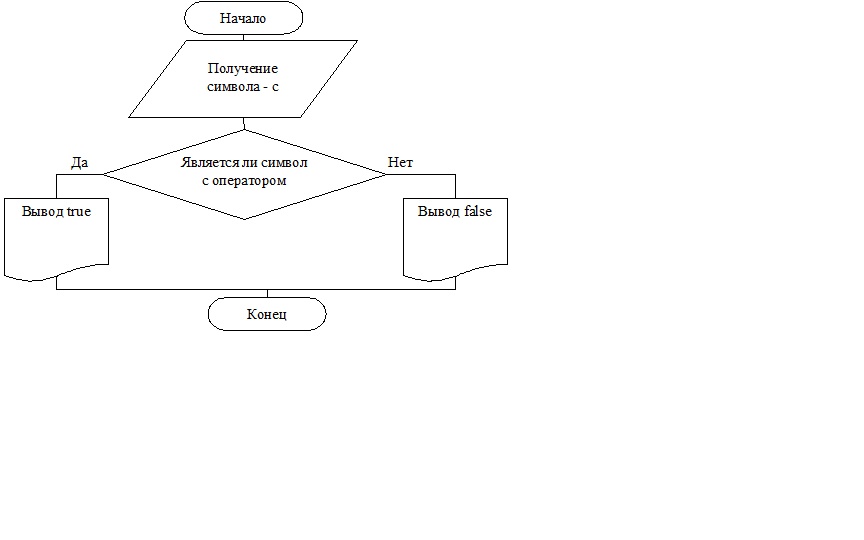
Рисунок 3. Блок-схема алгоритма IsOpperator
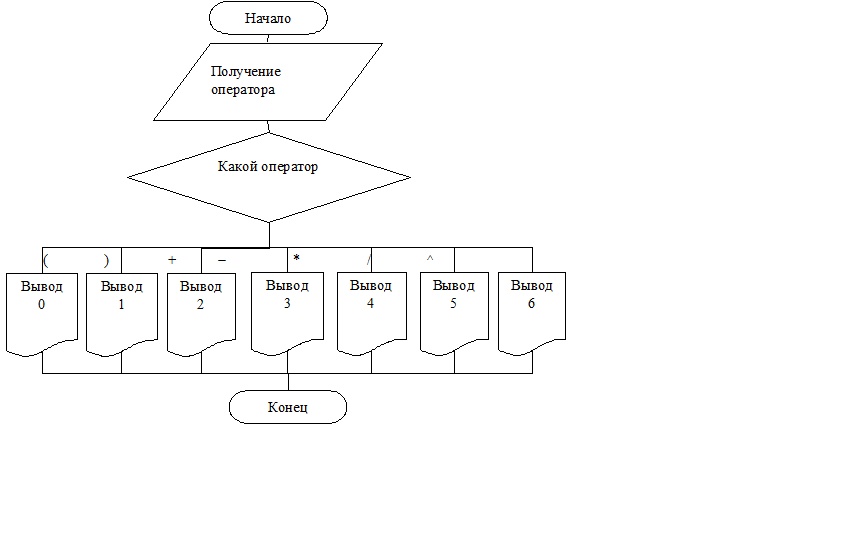
Рисунок 4. Блок-схема алгоритма GetPriority
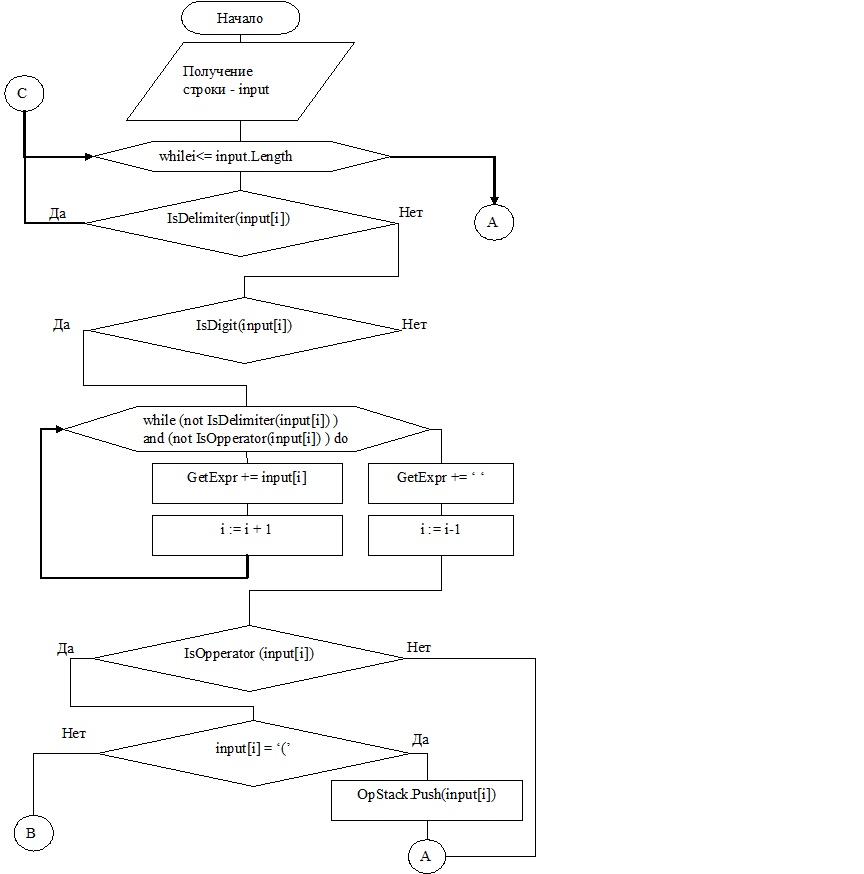
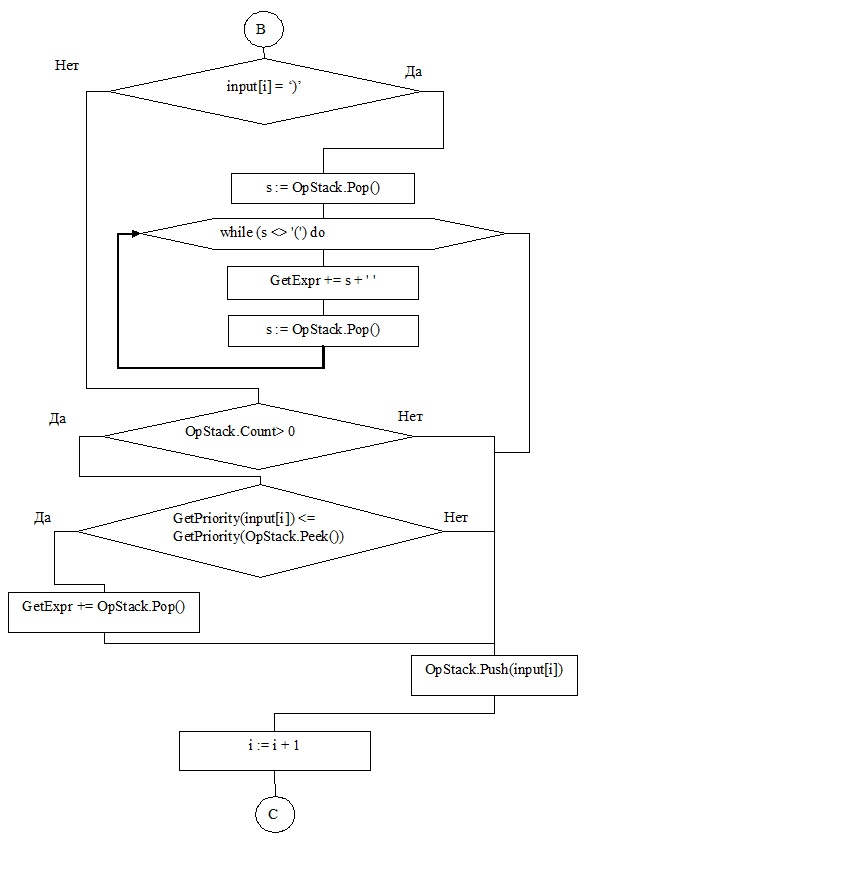
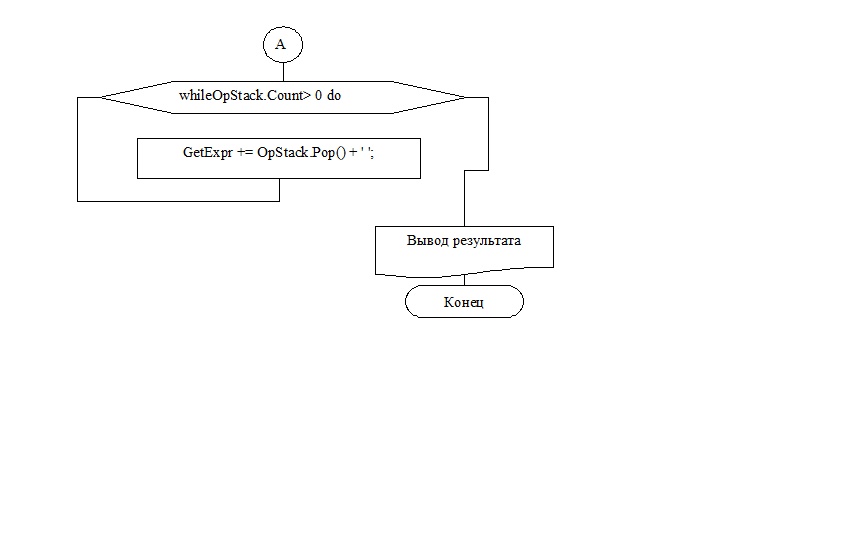
Рисунок 5. Блок-схема алгоритма GetExpr
В результате работы над проектом у школьников возникает проблемная ситуация: Каким образом перевести обычное выражение, заданное строкой символов в постфиксную форму? В случае трудностей в решении возможно предложить ученикам блок-схему, представленную рисунке 5.
На следующем этапе школьники разрабатывают программу, вычисляющую выражение в постфиксной записи (Рисунок 6).
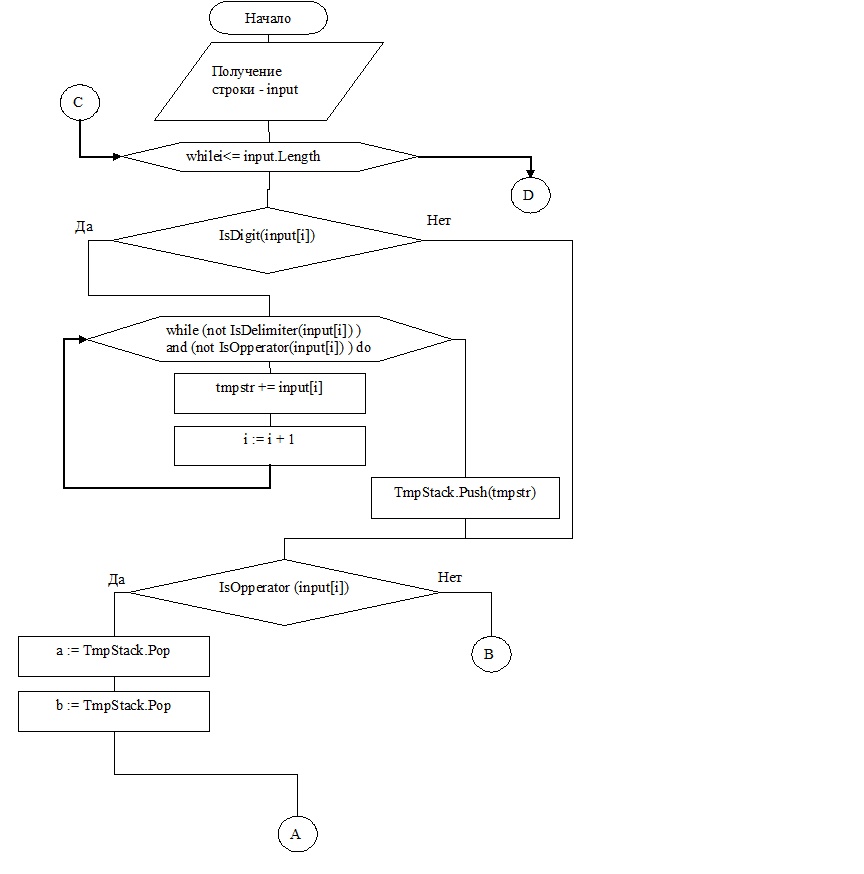
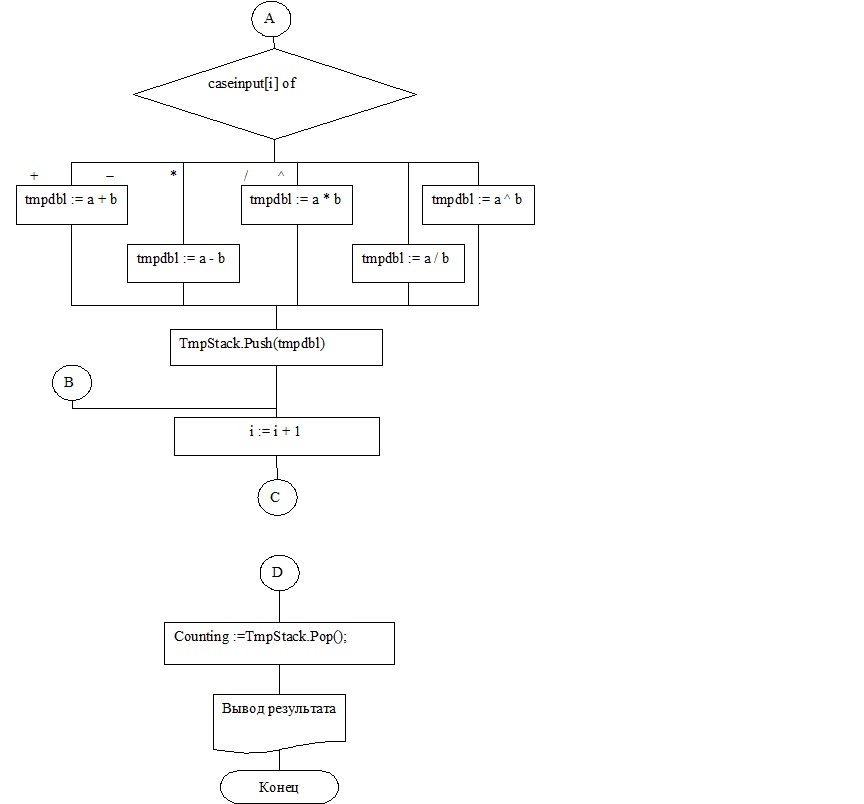
Рисунок 6. Блок-схема алгоритма Counting
На завершающем этапе школьники осуществляют сборку всех подпрограмм в программу Calculate (принимает выражение, проверяет и выводит результат) – Рисунок 7.
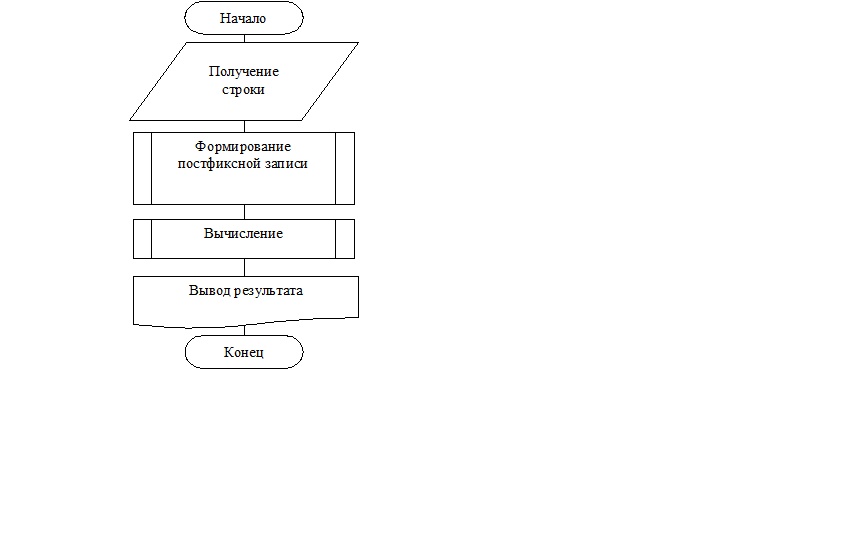
Рисунок 4. Блок-схема алгоритма Calculate
Время выполнения заданий сильно варьируется в зависимости от уровня учащихся: от 2 до 6 учебных занятий (уроков).
Таким образом, приведенный в настоящей статье материал позволяет эффективно организовать занятия школьников по решению задач повышенной сложности по программированию. В процессе разработки алгоритмов школьники овладеют компетенциями, связанными с технологиями программирования, организации и использования важнейших структур хранения данных, освоят использование подпрограмм.
В результате работы школьники создадут готовый программный продукт, обеспечивающий результативность образовательного процесса, освоят проектный тип организации деятельности.
ИНФОРМАЦИОННЫЕ ИСТОЧНИКИ
1. Можаров М.С., Валеева Ю.И., Попова Л.В. Практикум по решению задач в среде Lazarus с использованием модульно-рейтинговой системы оценивания: Учебно-методическое пособие для студентов. – Новокузнецк: изд-во КузГПА, 2013. – 150 с.
2. Можаров М.С., Бойченко Г.Н. Основы структурного программирования: Учебное пособие. – Новокузнецк: Изд-во КузГПА, 2006. – 220 с.
3. Можаров М.С., Коткин С.Д. О развитии содержательной линии «моделирование и формализация» в школьном курсе «информатика и икт» // Информатика и образование. 2010. № 4. С. 95-99.
4. Можаров М.С. Структурное программирование в примерах и решениях: Учебное пособие. Рекомендовано УМО ГОУ ВПО РГПУ им. А.И.Герцена в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлению 050200 Физико-математическое образование (Регистрационный номер рецензии №782 от 07.04.2010г.) / Новокузнецк, 2010.
5. Можаров М.С., Журавлёв С.В. Некоторые особенности преподавания программирования за рубежом //Актуальные вопросы современной науки. 2015. № 40. С. 122-132.
6. Обратная польская запись – [электронный ресурс] – http://habrahabr.ru/post/100869/
7. Структуры данных: общее понятие, реализация. Простейшие структуры данных: очередь, стек. Использование стека и обратная польская запись – [электронный ресурс] – http://www.intuit.ru/studies/courses/2193/67/lecture/1980?page=5
