ОРГАНИЗАЦИЯ НАУЧНО-ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЫ ШКОЛЬНИКОВ ПО ПРОГРАММИРОВАНИЮ ПО ТЕМЕ «ПОСТРОЕНИЕ ФРАКТАЛЬНЫХ КРИВЫХ»
Раздел: Материалы I Всероссийской очно-заочной практической конференции "Математика, физика, информатика:проблемы и перспективы современного образования" (Новокузнецк, февраль 2016)
Журнал: Проблемы и перспективы современного образования в области информатики и ИКТ
11 мая 2016 г.
Авторы: Можаров Максим Сергеевич , Коченевская С. А.
М. С. Можаров, С. А. Коченевская
ОРГАНИЗАЦИЯ НАУЧНО-ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЫ ШКОЛЬНИКОВ ПО ПРОГРАММИРОВАНИЮ ПО ТЕМЕ «ПОСТРОЕНИЕ ФРАКТАЛЬНЫХ КРИВЫХ»
Занятия по данной теме начинаются с теоретического материала, связанного с историей возникновения понятия «фрактал», их научного применения, практической функции фрактальных кривых в решении разнообразных задач, применения их в компьютерной графике и компьютерном моделирование.
Учащиеся знакомятся с примерами фракталов, их свойствами, геометрическим разбором и программой построения.
Для организации индивидуальных занятий и самостоятельной работы предлагается авторская подборка заданий двух уровней: простого и повышенной сложности.
На начальном этапе учащиеся находят сходства органических и неорганических форм в природе, объекты, образованные по аналогии друг с другом (облака, кора и крона деревьев, морские раковины, кровеносная система и многое другое). Школьники приходят к заключению, что случайные формы всех этих объектов можно описать определенным фрактальным алгоритмом.
Школьники анализируют применимость фракталов. Например, в медицине теория фракталов применяется для анализа электрокардиограмм.
Фрактальный анализ помогает в поиске и разработке залежей полезных ископаемых, расположение которых, зачастую, происходит по фрактальному механизму. Исследование тектоники и сейсмичности иногда тоже проводится с помощью фрактальных алгоритмов. Геофизика использует фрактальный анализ и фракталы для исследования климата. В физике фрактальные алгоритмы дают возможность точно описать и предсказать свойства твёрдых, пористых, губчатых тел. Это помогает в поиске новых материалов с полезными свойствами. В телекоммуникациях фрактальные кривые используют для разработки фрактальных антенн. В сетевых технологиях, доказывается самоподобие трафика, который передается по разнообразным сетям. В частности, это в большей степени касается речевых, аудио- и видеосервисов.
Лекционный материал носит метапредметный и межпредметный характер. Приведем фрагмент теоретического занятия по теме.
Термин «фрактал» появился благодаря Бенуа Мандельброту (Benoît B. Mandelbrot).Он сам ввел этот термин в семидесятых годах двадцатого века, заимствовав из латинского языка слово fractus, перевод которого звучит как «ломаный» или «дробленый». Сегодня под словом «фрактал» подразумевается графически построенное изображение структуры, которая при увеличении подобна сама себе.
Математический фундамент для появления самих фракталов закладывался еще задолго до рождения ученого, но свое развитие они начали только с внедрением вычислительной техники. В начале своей научной карьеры Бенуа работал в исследовательском центре корпорации IBM. В то время в центре вели работу над осуществлением передачи информации на расстояние. В ходе изучения проблемы ученые столкнулись с большими потерями, возникающими из-за шумовых помех. Для ученых было необходимо понять, как предсказывать появление шумовых помех в электросхемах, если статистический метод оказывался недостаточно эффективным.
Анализируя результаты замера шума, Бенуа заметил одну необычную закономерность - запись графиков шумов в разном масштабе выглядела одинаково. Аналогичная картина наблюдалась независимо от времени фиксации графиков. С каждым изменением масштаба графика картина постоянно повторялась.
Мандельброт еще при жизни утверждал, что он всего лишь играет с картинками, а не занимается формулами. Для ученого было просто любую алгебраическую задачу перевести в область геометрии, где, как он считал, верный ответ всегда очевиден. Неудивительно, что именно ученый с таким развитым пространственным мышлением стал прародителем фрактальной геометрии. Ведь понимание сущности фрактальных кривых происходим именно тогда, когда начинаешь исследовать рисунки и вникать в сам смысл необычных узоров.
Один из самых первых изображений фрактала был графической интерпретацией множества Мандельброта (рисунок 1), появившееся благодаря работам Гастона Мориса Жюлиа (Gaston Maurice Julia).
Этот математик заинтересовался, каким будет множество, если для определенного значения числа мы вычисляем по формуле новое, после этого подставляем новое значение в формулу и находим еще одно значение. Результатом является длинная последовательность чисел.
Для получения полного представления о данном множестве, нужно было сделать большое количество расчетов. Вручную это просчитать не представлялось возможным. Но с появлением мощных вычислительных устройств математики смогли гораздо меньше тратить времени на изучение интересующих их вопросов. Бенуа был первым, кто использовал компьютер для вычисления классического фрактала. После обработки результатов Мандельброт получил график.
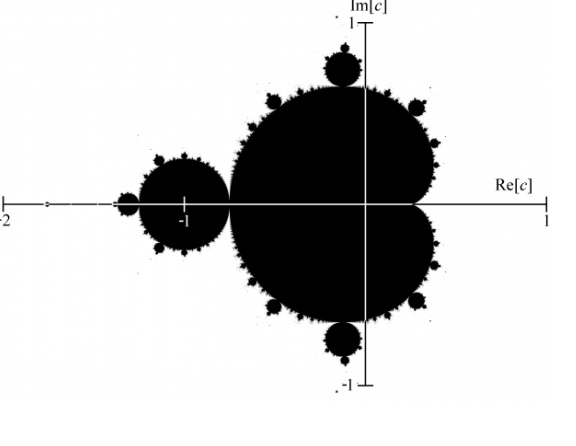
Рисунок 1. Множество Мандельброта
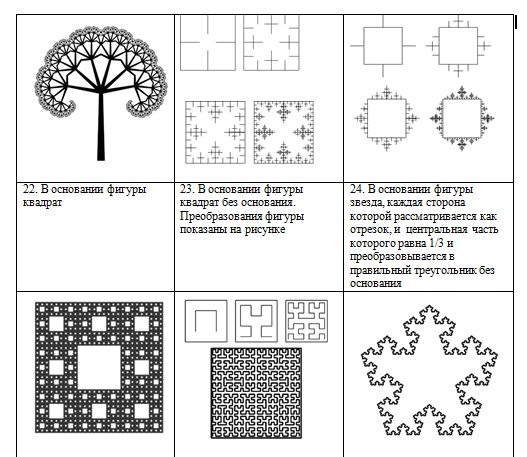
Изучив и осмыслив теоретический материал, учащиеся знакомятся с примерами фрактальных кривых. Изучают принципы их геометрического построения, разрабатывают алгоритм и программу построения.
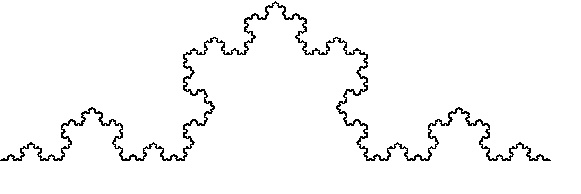
Рисунок 2. Результат работы программы построения кривой Коха
Кривая Коха (рисунок 2) имеет коэффициент подобия 1/3; также известно, что эта кривая нигде с собой не пересекается, так как вновь достраиваемые части кривой настолько малы, что не соприкасаются друг с другом.
Строится кривая с помощью разделения отрезка на три равные части и замены средней части этого отрезка на равносторонний треугольник без основания. Таким образом получается ломаная состоящая из четырех частей длиной 1/3 от прежнего отрезка. На следующем шаге операция повторятся для каждого из получившихся отрезков.
Программа, разработанная школьниками:
procedure koh(x1,y1,x2,y2, al : real);
var r,x3,y3,x4,y4,x5,y5 : real;
begin
r := sqrt(sqr(x2-x1)+sqr(y2-y1))/3;
if r <=1 then begin
paintbox1.canvas.line(round(x1),round(y1),round(x2),round(y2));
exit;
end;
x3 := (2*x1+x2)/3; y3 := (2*y1+y2)/3;
x4 := (x1+2*x2)/3; y4 := (y1+2*y2)/3;
x5 := x3+r*cos(al+pi/3); y5 := y3-r*sin(al+pi/3);
koh(x1,y1,x3,y3,al);
koh(x3,y3,x5,y5,al+pi/3);
koh(x5,y5,x4,y4,al-pi/3);
koh(x4,y4,x2,y2,al);
end;
begin
koh(10,300,300,300,0)
end;
Дерево Пифагора (рисунок 3).
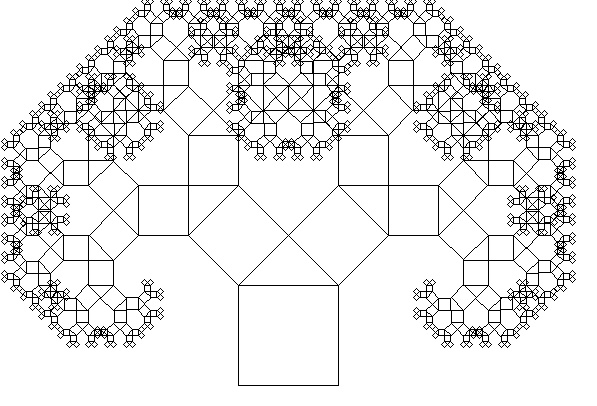
Рисунок 3. Результат работы программы построения кривой «Дерево Пифагора»
Пифагор, построил этот фрактал для доказательства своей теоремы. На верхней грани квадрата расположен прямоугольный, равнобедренный треугольник. Новые квадраты строятся на катетах треугольника.
Известно одно свойство этого дерева, если площадь нижнего квадрата будет равна единице, то площади квадратов на каждом следующем уровне тоже соответственно будут равны единице.
Программа, разработанная школьниками:
procedurepif(x1,y1,x2,y2,al : real);
var r,x3,y3,x4,y4,x5,y5 : real;
begin
r := sqrt(sqr(x2-x1)+sqr(y2-y1));
if r < 2 then exit;
x3 := x1 + r *cos(al+pi/2); y3 := y1 - r *sin(al+pi/2);
x4 := x2 + r *cos(al+pi/2); y4 := y2 - r *sin(al+pi/2);
x5 := x3 + (sqrt(2)*r/2)*cos(al+pi/4);
y5 := y3 - (sqrt(2)*r/2)*sin(al+pi/4);
paintbox1.canvas.line(round(x1),round(y1),round(x2),round(y2));;
paintbox1.canvas.line(round(x1),round(y1),round(x3),round(y3));;
paintbox1.canvas.line(round(x2),round(y2),round(x4),round(y4));;
paintbox1.canvas.line(round(x4),round(y4),round(x3),round(y3));;
paintbox1.canvas.line(round(x3),round(y3),round(x5),round(y5));;
paintbox1.canvas.line(round(x4),round(y4),round(x5),round(y5));;
pif(x3,y3,x5,y5,al+pi/4);
pif(x5,y5,x4,y4,al-pi/4);
end;
begin
pif(150,400,200,400,0);
end.
Итогом изучения темы «Построение фрактальных кривых» является самостоятельная работа школьников.
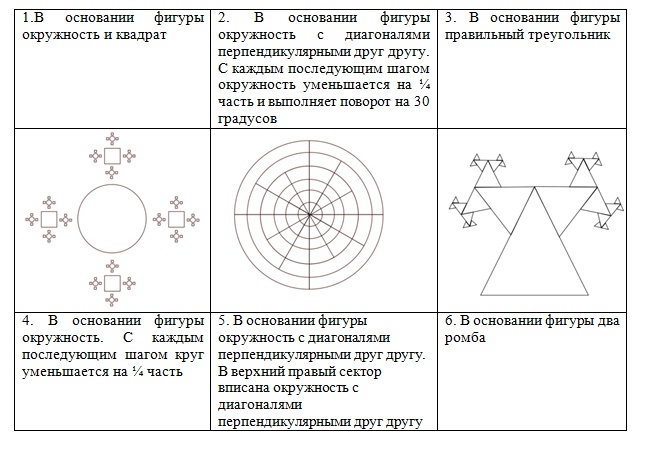
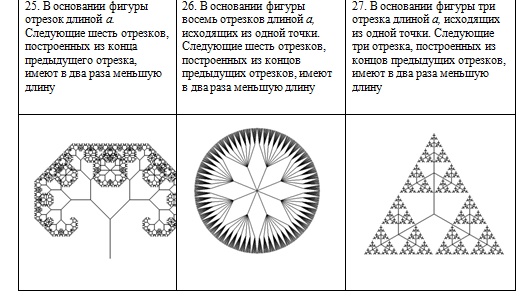
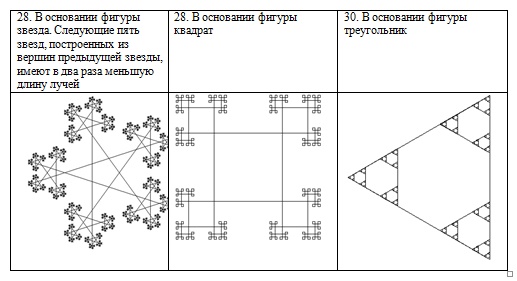
Задания для самостоятельной работы (1 уровень):
написать программу, выводящую на экран дисплея в графическом режиме следующие рекурсивные построения.
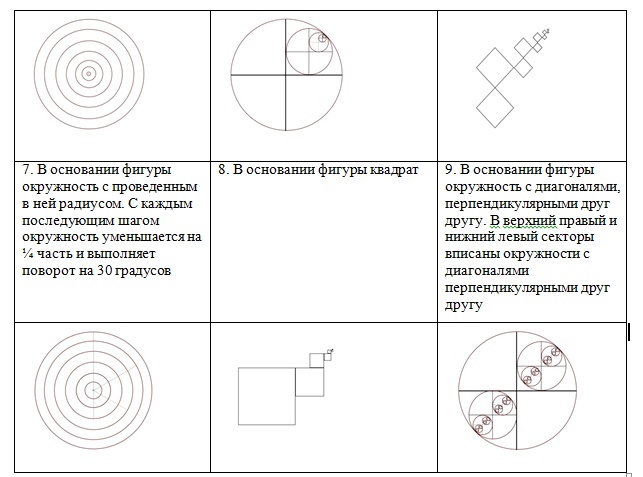
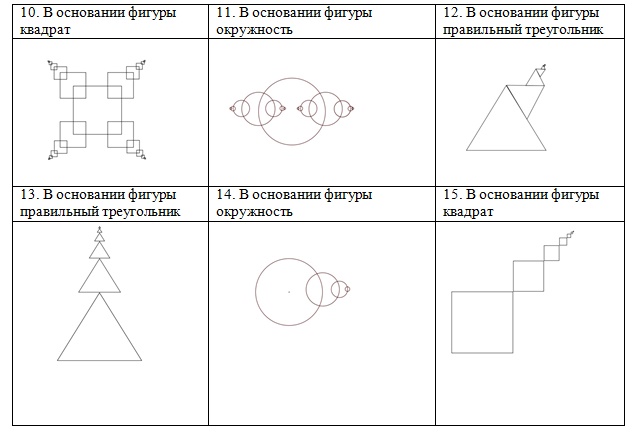
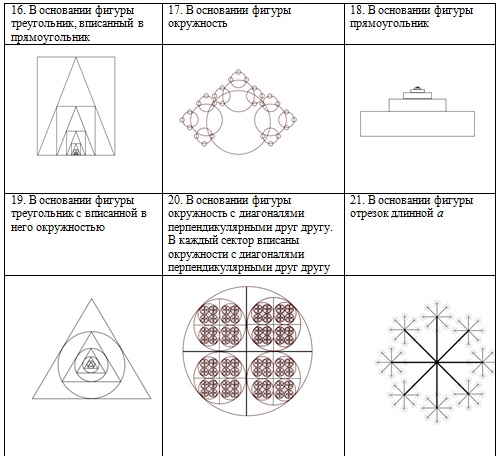
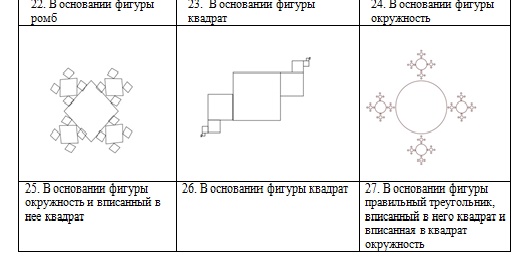
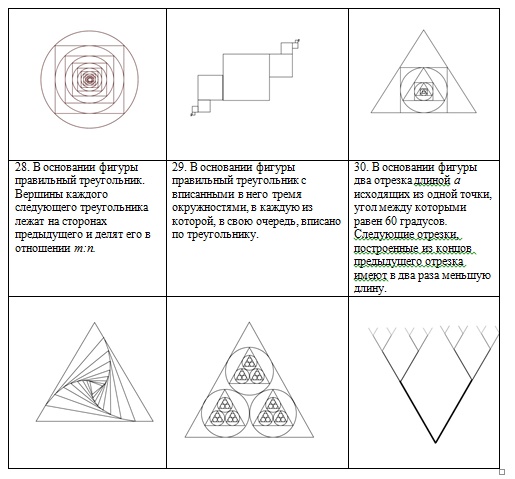
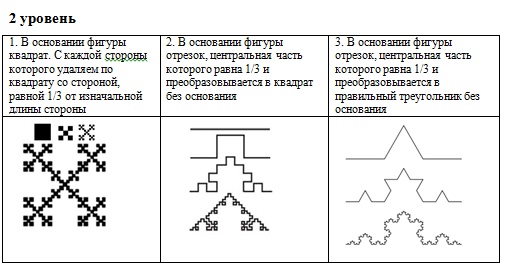

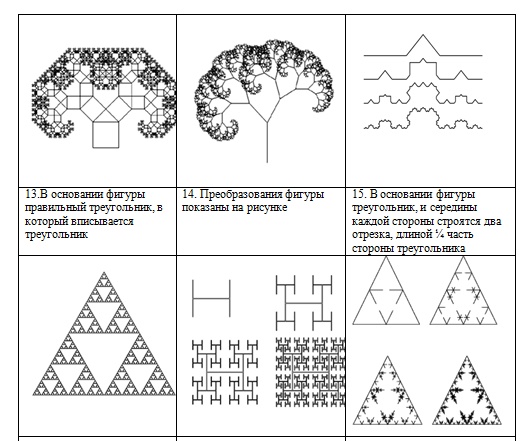
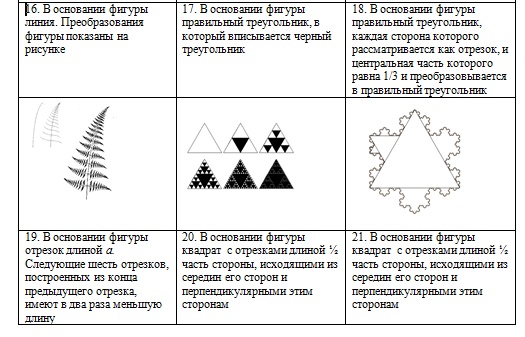
ИНФОРМАЦИОННЫЕ ИСТОЧНИКИ
1. Загадочный беспорядок: история фракталов и области их применения[Электронный ресурс]:3DNews URL:http://www.3dnews.ru/754657 (дата обращения:4.12.2015).
2. Задача № 3787. Кривая дракона [Электронныйресурс]: Дистанционная подготовка по информатике URL:http://informatics.mccme.ru/mod/statements/
view3.php?chapterid=3787(дата обращения:13.12.2015).
3. Рекурсия [Электронный ресурс]: Lazarus для школьников и студентовURL:https://sites.google.com/site/studylazarus/tasks/recursion (дата обращения:
20.12.2015).
4. Рекурсия Pascal-Паскаль [Электронный ресурс]: Программирование. Рекурсия. Паскаль.URL:http://www.pascal.helpov.net/index/recursion_pascal_programming (дата обращения:15.12.2015).
5. Снежинка Коха [Электронный ресурс]:Компьютерная графика URL:http://grafika.me/node/94 (дата обращения:18.12.2015).
6. Фрактальные кривые, деревья, растения, множества Кантора, множества Серпинского Паскаль [Электронный ресурс]:Fractalworld.URL:http://fractalworld.
xaoc.ru/List (дата обращения:7.12.2015).
7. Фракталы [Электронный ресурс]:Персональная страничка
Диканева Тараса Викторовича.URL: http://www.tvd-home.ru/recursion#p6_1(дата обращения:12.12.2015).
8. Можаров М.С., Валеева Ю.И., Попова Л.В. Практикум по решению задач в среде Lazarus с использованием модульно-рейтинговой системы оценивания: Учебно-методическое пособие для студентов. – Новокузнецк: изд-во КузГПА, 2013. – 150 с.
9. Можаров М.С. Структурное программирование в примерах и решениях// Учебное пособие. Рекомендовано УМО ГОУ ВПО РГПУ им. А.И.Герцена» в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлению 050200 Физико-математическое образование (Регистрационный номер рецензии №782 от 07.04.2010г.). Новокузнецк, 2010.
10. Можаров М.С., Журавлёв С.В. Некоторые особенности преподавания программирования за рубежом //Актуальные вопросы современной науки. 2015. № 40. С. 122-132.
