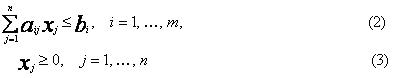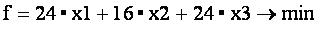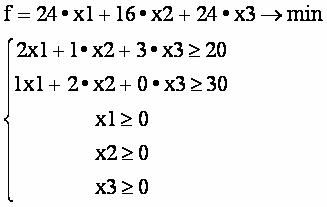РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ В ПРОГРАММЕ OPENOFFICE.ORG CALC
Раздел: Разработка методического обеспечения
Журнал: Использование и разработка программно-педагогических средств
3 февраля 2010 г.
Авторы: Буяковская Ирина Александровна
И. А. Буяковская
РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ В ПРОГРАММЕ OPENOFFICE.ORG CALC
Задачами математического программирования являются задачи выбора оптимального варианта решения среди возможных. Слово "программирование" заимствовано из зарубежной литературы, где оно используется в смысле "планирование". [1]
Подобные задачи возникают во многих областях человеческой деятельности: в экономике (планирование и управление экономическими объектами), в технике (выбор наилучшего проекта или оптимальной конструкции), в военном деле (при планировании боевых операций и управлении войсками). Источником задач математического программирования также являются и другие разделы математики, например, теория приближений и математическая статистика. [2]
Линейное программирование является разделом математического программирования, рассматривающим теорию и методы решения задач об экстремумах линейных функций на множествах, задаваемых системами линейных неравенств и равенств.
Типичной задачей линейного программирования является следующая: найти максимум линейной функции
при условиях
где cj, aij, bi- заданные числа.
Задачи линейного программирования являются математическими моделями задач технико-экономического содержания. Например: предприятие может выпускать n видов продукции; прибыльность единицы продукции вида j, j=1, ..., n, составляет cj. В производстве используются ресурсы m видов (сырье, рабочая сила, энергия и т.п.). Наличие ресурса i, i=1, ..., m, ограничено величиной bi. Расход ресурса i на производство единицы продукции вида j составляет aij. Требуется найти объемы выпуска xj по каждому из видов продукции таким образом, чтобы лимиты по ресурсам не были превышены, а суммарная прибыль была бы максимальной. Запись этих требований приводит к задаче (1)-(3).
Причем данную функцию (1) принято называть целевой функцией (или критерием оптимальности, критерием эффективности), а условия (2) и (3) - ограничениями данной задачи. Совокупность чисел X=(x1, x2, ..., xn) , удовлетворяющих ограничениям задачи, называется допустимым решением задачи (или планом). План, при котором целевая функция задачи принимает свое максимальное (минимальное) значение, называется оптимальным.
Приступая к решению задачи необходимо создать ее математическую модель.
Для построения математической модели необходимо ответить на следующие три вопроса [1]:
1. Что является искомыми величинами, то есть переменными этой задачи?
2. В чем состоит цель, для достижения которой из всех допустимых значений переменных нужно выбрать те, которые будут соответствовать наилучшему, то есть оптимальному, решению?
3. Какие ограничения должны быть наложены на переменные, чтобы выполнялись условия, описанные в задаче?
Рассмотрим решение задачи линейного программирования на конкретном примере:
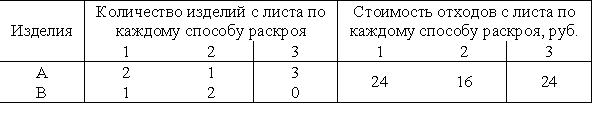
Условие задачи: Необходимо составить план раскроя с минимальными отходами изделий двух видов. Потребность в изделии первого вида не менее 20 шт., второго - не менее 30 шт.
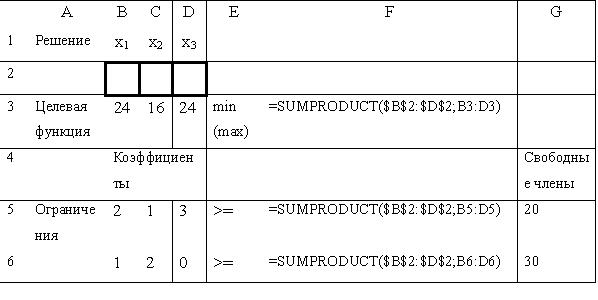
Введем переменные x1 - количество листов, раскроенных по первому типу, x2 - количество листов, раскроенных по второму типу, x3 - количество листов, раскроенных по третьему типу. Тогда 24∙x1 - стоимость отходов с листов, раскроенных по первому типу, 16∙x2 - стоимость отходов с листов, раскроенных по второму типу, 24∙x3 - стоимость отходов с листов, раскроенных по третьему типу. В результате получим целевую функцию
Учитывая, что потребность в изделии первого вида не менее 20 шт., второго - не менее 30 шт., получим ограничение 2:∙x1 + 1∙x2 + 3∙x3 ≥ 20, аналогично 1:∙x1 + 2∙x2 + 0∙x3 ≥ 30 получается второе ограничение. На переменные накладывается условие неотрицательности.
Таким образом, получим следующую математическую модель:
Решение задачи с помощью OpenOffice.org Calc
Запустите программу OpenOffice.org 3.1.1 Calc (Программы, задачи и сеансы - Офис - Электронная таблица (OpenOffice.org)) и создайте новую книгу. Далее подготовьте исходные данные на листе OpenOffice.org (вставьте необходимые коэффициенты, значения целевой функции, значения свободных членов и в столбец F вставьте функции SUMPRODUCT с абсолютной адресацией на строку 2, где будут отображены искомые значения x).
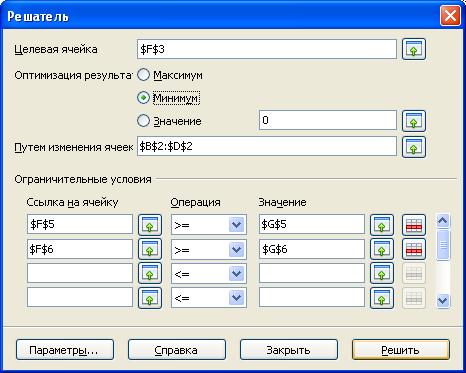
Выберите команду Сервис-Поиск решения, в появившемся диалоговом окне (рис.1) вводим следующие значения:
Рис. 1. Диалоговое окно «Поиск решения».
- в поле «Целевая ячейка» вводим адрес ячейки $F$3, в данной ячейке будет найдено оптимальное решение функции;
- в поле «Оптимизация результата» выбираем «Минимум»;
- в поле «Путем изменения ячеек» вводим диапазон ячеек $В$2:$D$2, в которых будут отображены искомые значения неизвестных х1, х2, х3;
- Вводим ограничительные условия $F$5>=$G$5, $F$6>=$G$6. В ячейках F5 и F6 появятся значения левых частей ограничений.
- Щелкаем по кнопке «Параметры» и ставим «Принять переменные как не отрицательные».
- Выполним процедуру, щелкнув по кнопке «Решить».
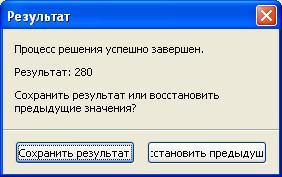
Если решение будет найдено, то появится сообщение: «Процесс решения успешно завершен».
Рис. 2. Диалоговое окно «Результат».
Выбрав «Сохранить результат», получим таблицу результатов.
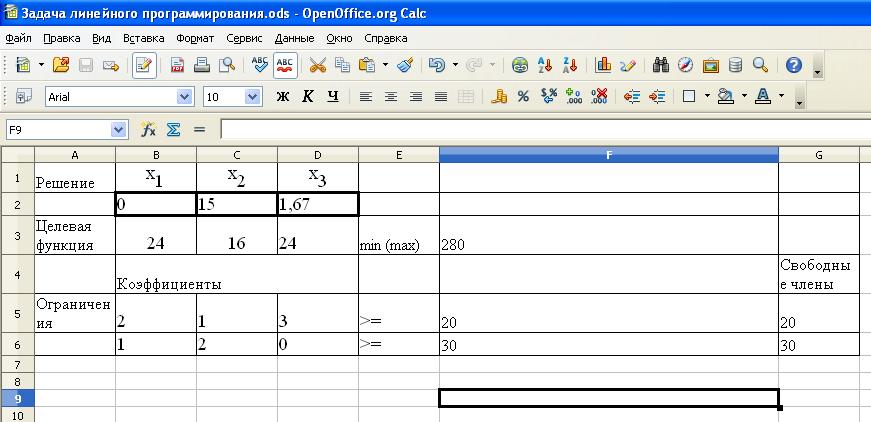
Рис. 3. Таблица с результатом решения задачи.
Таким образом, для получения минимальных отходов необходимо: 15 листов раскроить по второму способу, 1,7 листов раскроить по третьему способу. Минимальная стоимость отходов 280.
Для контроля усвоения пройденного материала обучающимся предлагается ответить на следующие вопросы:
- Что такое математическое и линейное программирование?
- Какие задачи являются задачами линейного программирования?
- Что представляют собой целевая функция, план и ограничения задачи?
- Какой план называется оптимальным?
- В чем заключается построение математической модели решения задачи линейного программирования?
- Каким образом решается задача с помощью OpenOffice.org Calc?
Список литературы:
- Алесинская Т.В., Сербин В.Д., Катаев А.В. Учебно-методическое пособие по курсу «Экономико-математические методы и модели. Линейное программирование». Таганрог: Изд-во ТРТУ, 2001. 79 с.
- Математический энциклопедический словарь. / Гл. ред. Ю.В. Прохоров; Ред. кол.: С.И. Адян, Н.С. Бахвалов, В.И. Битюцков, А.П. Ершов, Л.Д. Кудрявцев, А.Л. Онищик, А.П. Юшкевич. - М.: Сов. энциклопедия, 1988. - 847 с.