ИЗУЧЕНИЕ КУРСА «УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ» С ПРИМЕНЕНИЕМ МАТЕМАТИЧЕСКОГО ПАКЕТА MATHCAD
Раздел: Материалы I Всероссийской очно-заочной практической конференции "Математика, физика, информатика:проблемы и перспективы современного образования" (Новокузнецк, февраль 2016)
Журнал: Проблемы и перспективы современного математического образования
6 июня 2016 г.
Авторы: Фураев В. З.
В. З. Фураев
ИЗУЧЕНИЕ КУРСА «УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ» С ПРИМЕНЕНИЕМ МАТЕМАТИЧЕСКОГО ПАКЕТА MATHCAD
Дисциплина «Уравнения математической физики» является одной из важной среди классических примеров описания и математического моделирования физических явлений.
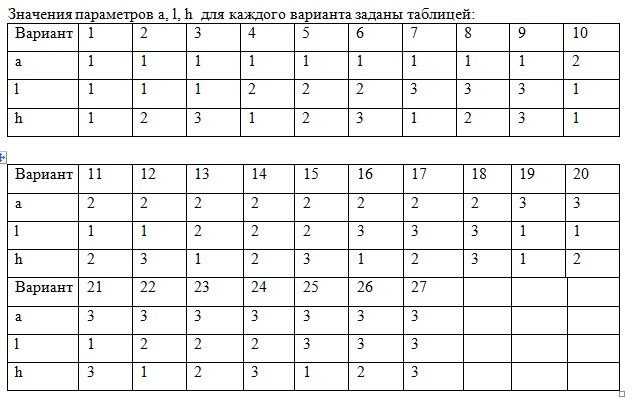
Указанный раздел изучается студентами 4 курса специальности «Математика и информатика» в 7 семестре в объёме 18 часов лекционных и 18 часов практических занятий, а также студентами 4 курса ЗФО специальности «Математика» в объёме 2 часов лекционных и 4 часов практических занятий с последующей сдачей зачета.
Для зачета требуется графическое представление решений задач Коши для одномерного волнового уравнения и уравнения теплопроводности, а также аналитическое и графическое представления решений соответствующих классических начально-краевых задач.
Если на дневном отделении число отведенных на данную дисциплину часов можно считать приемлемым для овладения основными навыками решения указанных задач, то на отделении ЗФО при традиционном подходе число аудиторных занятий явно недостаточно.
В помощь студентам, изучающим курс уравнений математической физики, в 2008 г. издано учебно-методическое пособие [1], основой которого является широкое использование пакета математических программ MathCad.
В указанном пособии выводится уравнение колебаний струны и уравнение теплопроводности стержня, приведены постановки начально-краевых задач, формулы Даламбера и Пуассона решений задачи Коши для соответствующих уравнений, формулы решения основных начально-краевых задач, получаемых методом Фурье разделения переменных. Приведены примеры решения основных задач классической математической физики. Всё это позволяет студентам достаточно успешно выполнить индивидуальные зачетные задания. Однако при этом они должны овладеть элементарными методами программирования в среде MathCad. Впрочем, для выполнения контрольных заданий у студента есть выбор в использовании других вычислительных средств.
Примеры контрольных индивидуальных заданий.
Задание 1. Решите задачу Коши для волнового уравнения.
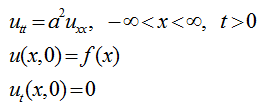
Если 1) 
2) 
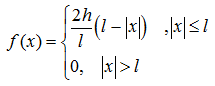
3) 
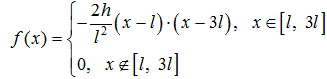
Постройте графики функций 
для значений времени 
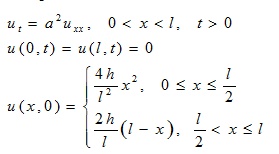
Задание 3.2. Решите первую краевую задачу для уравнения теплопроводности на отрезке:
Постройте графики распределения температур для 
Примеры решения задач в среде MathCad.
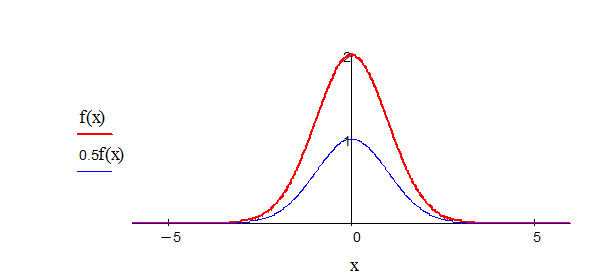
Задание 1. Пусть начальная форма струны задана формулой:
.
Профили струны в моменты времени t определяется формулой Даламбера (волны отклонения)
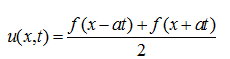
и в различные моменты времени имеют вид:
t=0.2
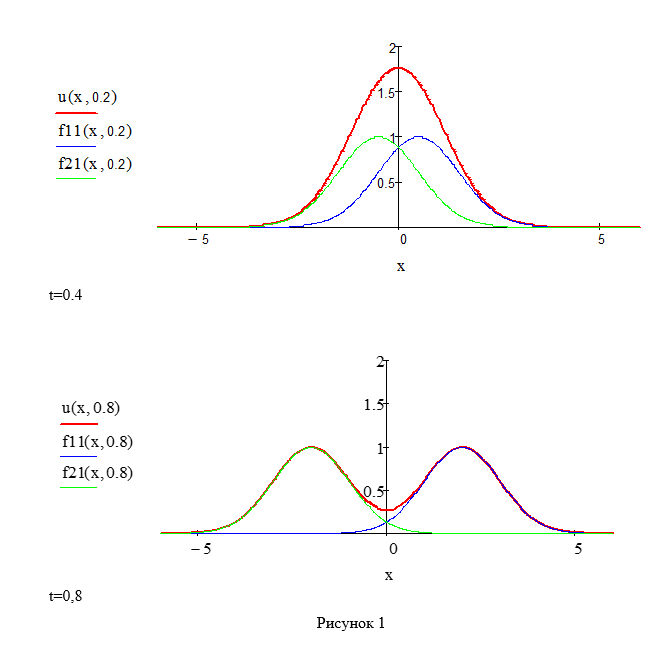
Таким образом, начальное отклонение от положения равновесия струны распадается на две полуволны, разбегающиеся в противоположных направлениях со скоростью а.
Решение задачи представляется в форме
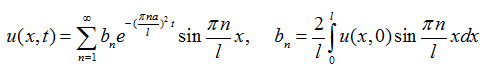
где 
- коэффициенты Фурье разложения начальной функции в ряд Фурье по синусам на отрезке 
.
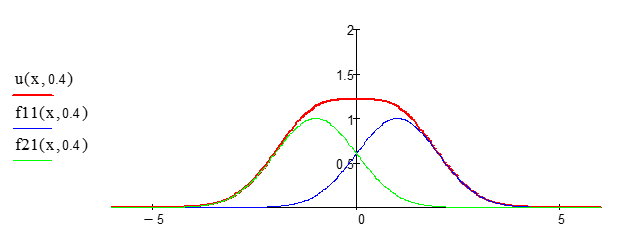
Графики распределения температуры по времени в стержне, на концах которого поддерживается постоянная нулевая температура, приводятся на рис. 2.
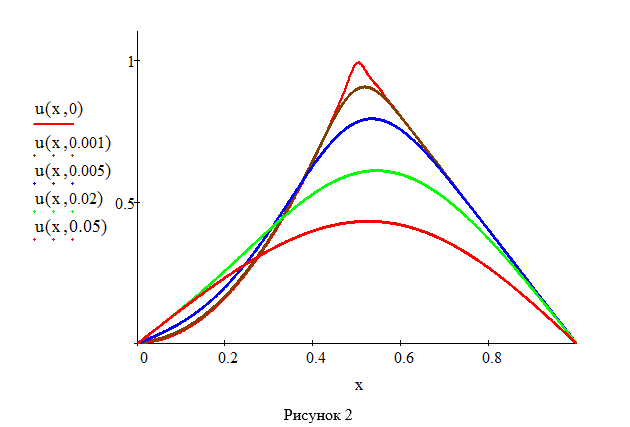
C другими примерами решений начально-краевых задач можно ознакомиться в учебно-методическом пособии [1].
Приведенные примеры показывают, что программные средства используемого математического пакета позволяют получать наглядные представления об изучаемом физическом процессе, изучать зависимость решений как от начальных и граничных условий, так и от параметров, входящих в дифференциальные уравнения, описывающих волновые процессы и процесс теплопроводности.
Помимо оптимизации во времени процесса изучения курса уравнений математической физики, к достоинствам данного метода можно отнести и тот факт, что описываемые явления можно проследить в динамике их развития во времени путем построения анимационных видеоклипов.
Однако следует отметить, что построение графиков решений краевых задач не должно быть основной целью при изучении указанного курса, главными здесь всё же остаются методы решений и построение решений начально-краевых задач в аналитической форме.
ИНФОРМАЦИОННЫЕ ИСТОЧНИКИ
1. Фураев В.З. Введение в уравнения и методы математической физики. Учебно-методическое пособие. – Новокузнецк: РИО КузГПА, 2008. – 83 с.
2. Тихонов А.Н., Самарский А.А. Уравнения математической физики.- М.: Наука, 1972. – 735 с.