ОБУЧЕНИЕ РЕШЕНИЮ ЗАДАЧ ПОВЫШЕННОЙ СЛОЖНОСТИ МЕТОДОМ АФФИННЫХ ПРЕОБРАЗОВАНИЙ В ШКОЛЬНОМ КУРСЕ ГЕОМЕТРИИ
Раздел: VI Всероссийская научно-практическая конференция студентов, аспирантов и молодых ученых. Секция "Математика, теория и методика преподавания математики и физики"
Журнал: Научно-исследовательская работа студентов ФМиТЭФ НИФ КемГУ
29 сентября 2016 г.
Авторы: Качесов Н. Е.
Н. Е. Качесов
ОБУЧЕНИЕ РЕШЕНИЮ ЗАДАЧ ПОВЫШЕННОЙ СЛОЖНОСТИ МЕТОДОМ АФФИННЫХ ПРЕОБРАЗОВАНИЙ В ШКОЛЬНОМ КУРСЕ ГЕОМЕТРИИ
Одной из основных целей изучения математики на профильном уровне является формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов. Включение в систему заданий ЕГЭ геометрических задач повышенного уровня сложности актуализирует проблему обучения таким методам решения задач, которые являлись бы “универсальными”, т.е. позволяли охватить как можно более широкий класс задач. Одним из таких методов является метод аффинных преобразований.
Преобразование плоскости (или пространства), при котором каждая прямая переходит в прямую, называется аффинным. Аффинные преобразования сохраняют параллельность прямых, простое отношение троек коллинеарных точек и вообще отношение длин параллельных отрезков (с учетом их направления), отношение площадей фигур (лежащих в одной плоскости или в параллельных плоскостях) в случае преобразований пространства и отношение объёмов тел.
Если в плоскости даны два произвольных треугольника ABC и A1B1C1, то существует одно и только одно аффинное преобразование плоскости, переводящее вершины первого треугольника с соответствующие вершины второго. Если ввести две системы косоугольных координат с началами в точках A и A1 и единичными отрезками осей AB, AC и A1B1, A1C1 соответственно, то точка с координатами (x, y) относительно первой системы перейдет в точку с такими же координатами относительно второй системы.
Если образом данного треугольника при аффинном преобразовании может быть совершенно произвольный треугольник, то образом квадрата (как и вообще параллелограмма) будет произвольный параллелограмм, образом окружности – эллипс.
Обычно, задачу можно решить методом аффинных преобразований, если нужно найти отношение длин, отношение площадей, доказать параллельность или принадлежность точек одной прямой. Причем в условии задачи не должны содержаться данные, не сохраняющиеся при аффинных преобразованиях.
Свойства фигур называются аффинными, если они сохраняются при аффинных отображениях. Например, быть медианой треугольника - это аффинное свойство (середина стороны переходит в середину при аффинном отображении), а быть биссектрисой – нет.
Суть метода аффинных преобразований: при решении задач на аффинные свойства перейти с помощью аффинных преобразований к более простым фигурам, например, к правильному треугольнику, квадрату, равнобедренной трапеции. А затем с помощью обратного аффинного преобразования перенести полученный результат на искомую фигуру.
С помощью аффинных преобразований можно доказать теорему о точке пересечения медиан треугольника, о четырех точках трапеции. В методической литературе приведены примеры решения задач ЕГЭ, а также олимпиадных задач с помощью метода аффинных преобразований.
Одной из актуальных проблем методики обучения математике является проблема организации учебных исследований школьников. Учебное исследование – это вид познавательной деятельности, который основан на выполнении учебных заданий, предполагающих самостоятельное выявление учащимися новых для них знаний, способов деятельности и направленных на достижение целей обучения. Учебное исследование способствует формированию следующих умений:
- добывать новые предметные знания, приемы и способы действий;
- самостоятельно организовывать поиск;
- достигать поставленных целей обучения;
- формировать мыслительные операции, такие как аналогия, классификация, обобщение и т.п.
Одним из средств организации учебных исследований являются задания на экспериментирование.
Наблюдение, опыт, измерения должны быть направлены на создание в процессе обучения специальных ситуаций и предоставление учащимся возможности извлечь из них очевидные закономерности, геометрические факты, идеи доказательства и т.д. Чаще всего результаты наблюдений, опыта и измерений служат посылками индуктивных выводов, с помощью которых осуществляются открытия новых истин. В геометрии можно выделить следующие виды эксперимента:
1) вычислительный;
2) экспериментирование на моделях
3) компьютерный эксперимент
4) мысленный эксперимент.
В своей работе особое внимание мы уделяем компьютерному эксперименту. Компьютерный эксперимент — это эксперимент над математической моделью объекта исследования на ЭВМ, который состоит в том что, по одним параметрам модели вычисляются другие ее параметры и на этой основе делаются выводы о свойствах объекта, описываемого математической моделью.
Новые компьютерные технологии ведут к поистине революционному перевороту в возможностях геометрических экспериментов. Они позволяют перейти от философии "давать знания" к философии "учить добывать знания".
Динамическая геометрия предназначена для того, чтобы превратить геометрию из теоретического, оперирующего аксиомами и теоремами предмета в экспериментальный курс. Главной идеей применения на уроках любой программы, реализующей идеи динамической геометрии, является "открытие" учащимися геометрических закономерностей, возможность проведения компьютерного геометрического эксперимента. Динамическая геометрия – это обучающая и развивающая среда, используемая для различных геометрических построений и экспериментов. Она предоставляет возможность успешной работы учащимся различных уровней подготовки.
При варьировании динамического чертежа гораздо легче выделить те свойства рассматриваемой конфигурации, которые являются неизменными, т.е. следствия условий, накладываемых на исходную фигуру, – например, заметить, что какие-то прямые всегда параллельны или какие-то отрезки равны. Компьютерный эксперимент может подсказать решение задачи, а может помочь опровергнуть какие-то предположения, кажущиеся вполне правдоподобными.
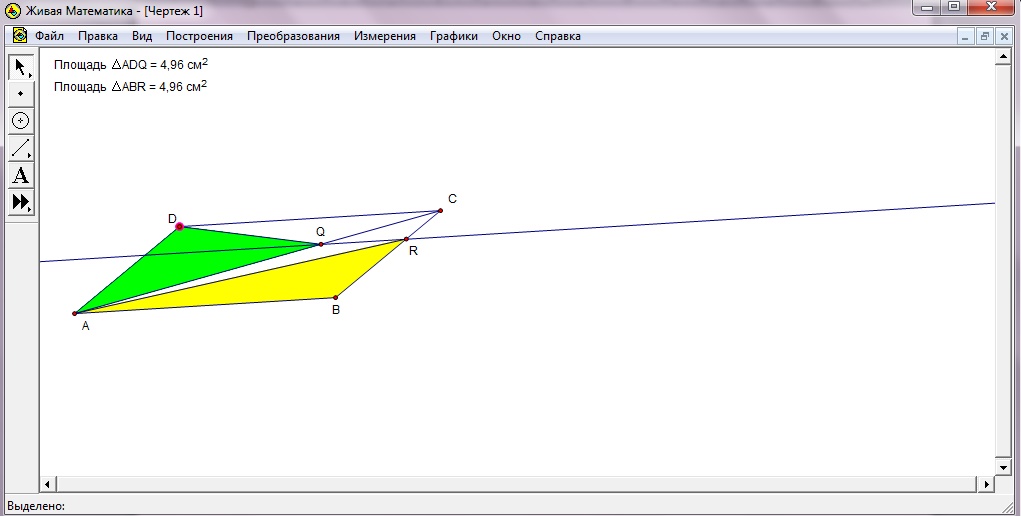
Рассмотрим пример задания на экспериментирование, реализуемого в компьютерной программе “Живая математика” с применением метода аффинных преобразований.
Задача. Через точку Q диагонали АС параллелограмма АВСD проведена прямая l, параллельная АВ и пересекающая сторону ВС в точке R. Сравните площади треугольников АВR и ADQ. Сформулируйте задачу на доказательство. Докажите сформулированное утверждение.
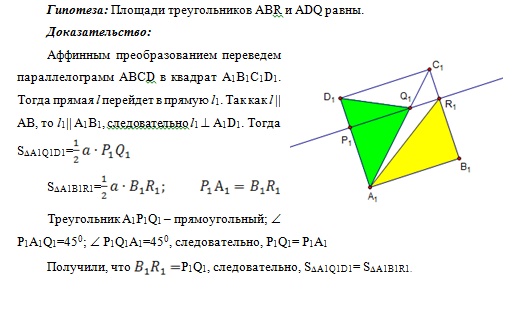
Изменяя форму и размеры четырехугольника АВСD, т.е. наблюдая геометрическую конфигурацию в динамике, и вычисляя площади треугольников АВR и ADQ, учащиеся высказывают гипотезу о равенстве этих площадей.

Список литературы
- Примаков, Д. А. Геометрия и топология: учеб. пособие / Д. А. Примаков, Р. Я. Хамидуллин. - 2-е изд., перераб. и доп. - Москва: МФПА, 2011. - 272 с.
- Каюмов, О.Р. Преобразования плоскости и их применение к решению задач планиметрии : учебное пособие / О.Р. Каюмов. - 2-е изд.,испр. и доп. - М. : Флинта, 2014. - 133 с.
- Понарин, Я.П. Аффинная и проективная геометрия / Я.П. Понарин. - М. : МЦНМО, 2009. - 288 с..
- Ходот, Т. Г. Задачи по геометрии : учеб. пособие для студ. высш. пед. учеб. заведений/ Т. Г. Ходот, И. Д. Захарченко, А. Б. Михайлова. – М.: Издательский центр «Академия», 2006.- 256 с.
Научный руководитель:
кандидат педагогических наук Позднякова Е.В.
