ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКОГО ПАКЕТА MATHCAD К РЕШЕНИЮ СИСТЕМ УРАВНЕНИЙ С ПАРАМЕТРОМ
Раздел: Материалы II Международной очно-заочной научно-практической конференции «Проблемы и перспективы современного физико-математического, информационного и технологического образования» (Новокузнецк, февраль 2018)
Журнал: Проблемы и перспективы современного физико-математического образования
27 февраля 2018 г.
Авторы: Фомина Анжелла Владимировна , Фураев В. З.
УДК 517.912:004.9
А. В. Фомина, В. З. Фураев
A. V. Fomina, V. Z. Furaev
Фомина Анжелла Владимировна, кандидат физико-математических наук, доцент, НФИ КемГУ, г. Новокузнецк.
Фураев Валерий Зиновьевич, кандидат физико-математических наук, доцент, НФИ КемГУ, г. Новокузнецк.
Fomina Anzhella Vladimirovna, Candidate of Physical and Mathematical Sciences, Associate Professor, NBI KemSU, Novokuznetsk.
Furaev Valeriy Zinovievich, Candidate of Physical and Mathematical Sciences, Associate Professor, NBI KemSU, Novokuznetsk.
ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКОГО ПАКЕТА MATHCAD К РЕШЕНИЮ СИСТЕМ УРАВНЕНИЙ С ПАРАМЕТРОМ
APPLICATION OF THE MATHCAD MATHEMATICAL PACKAGE TO THE SOLUTION OF SYSTEMS OF EQUATIONS WITH PARAMETER
Аннотация. В работе рассматривается решение систем уравнений с параметром с использованием математического пакета MathCad.
Annotation. The paper deals with the solution of systems of equations with a parameter using the mathematical package MathCad.
Ключевые слова: параметр, система уравнений, решение, график функции, семейство прямых, визуализация.
Keywords: parameter, system of equations, solution, function graph, family of lines, visualization.
Согласно спецификации контрольных измерительных материалов единого государственного экзамена по математике задача с параметром относится к высокому уровню сложности в системе заданий ЕГЭ. Умение решать задачи с параметрами демонстрирует владение методами решения различных уравнений, неравенств и их систем, в том числе и графическим методом. Задачи с параметрами, связанные с разрешимостью и числом решений уравнений, неравенств и их систем, наиболее удобно решать именно графическим методом. Предложенный в работе подход к решению задач с параметрами может быть рекомендован учащимся старших классов, владеющих навыками работы с математическими пакетами прикладных программ, для контроля самостоятельной подготовки к ЕГЭ. Применение математического пакета MathCad к решению систем уравнений с параметрами иллюстрируется на примерах решения задач из вариантов единого государственного экзамена в 2015 году.
Рассмотрим следующую задачу [1]:
Найдите все значения a, при каждом из которых система уравнений
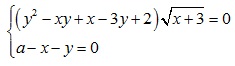(1)
имеет ровно два различных решения.
Решение системы может быть найдено с помощью приведенного ниже вычислительного блока [2]:
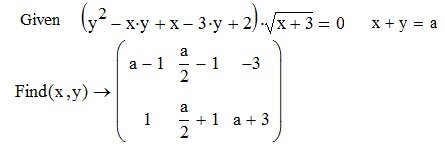
Однако решения выдаются без учета области допустимых значений переменных и могут служить лишь основой для дальнейших исследований и проверки результатов рассуждений.
Разложим левую часть первого уравнения на множители
.
Множество допустимых значений описывается неравенствами
.
В указанной области значений переменных строим графики функций: y=1, y=x+2; y(x, a)=a-x, a=0,-2,-4 (рис. 1).
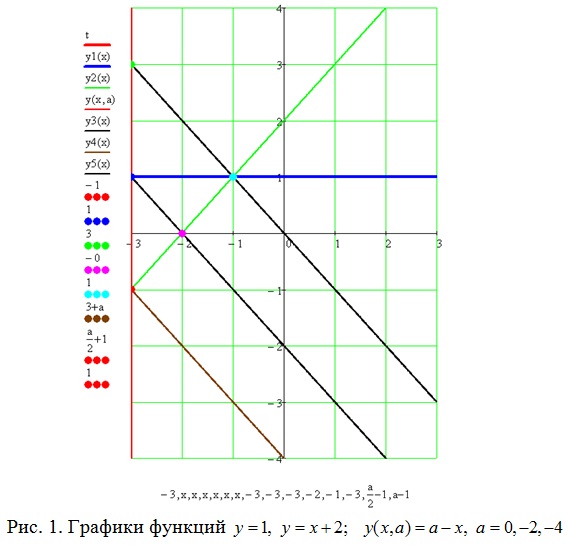
Число решений системы определяется количеством точек пересечения семейства прямых y(x, a)=x+a с графиками функций y=1, y=x+2 и прямой x=-3.
Для a≤-4 система имеет единственное решение x=-3, y=a+3. Для значений параметра -4<a≤-2, a="0"> </a≤-2,>
Для – три решения, указанные в приведенном выше в вычислительном блоке.
Рассмотрим еще один пример [1].
Найдите все значения а, при каждом из которых система
Строим графики функций y=5, y=x+2, y(x, a)=a(x-6) с учетом области допустимых значений переменных (рис. 2).
Решение также может быть найдено применением вычислительного блока [2]:
,
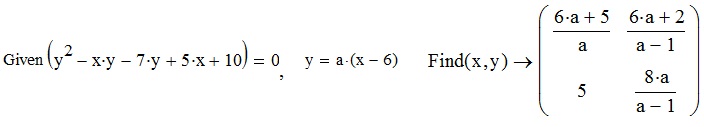Из результатов которого ясно, что для а = 1 система решений не имеет.
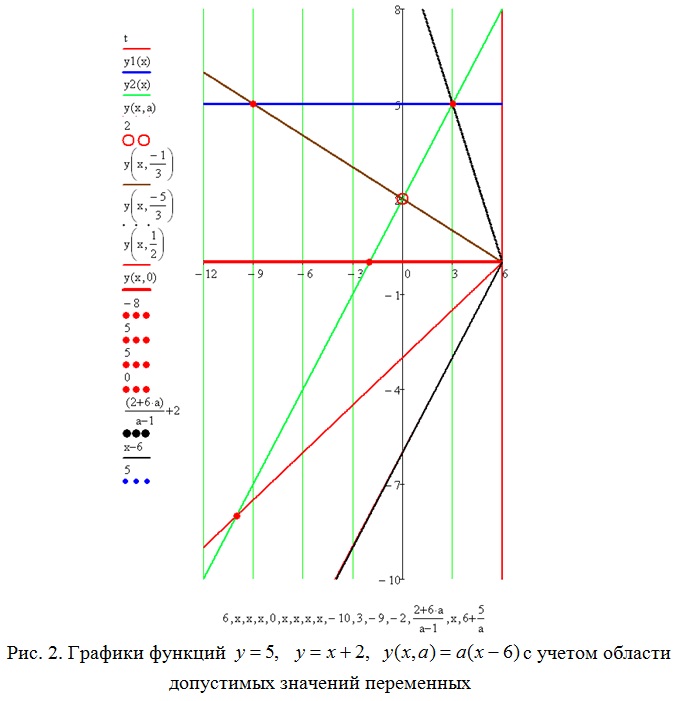
Для значений 
, так же как и для a=-5/3, при этом x=3, y=5. При a=-1/3 система имеет также одно решение x=-9, y=5, т.к. точка (0, 2) не входит в область допустимых значений переменных.
Преобразование же системы (2) в (3) производится в среде MathCad:
.
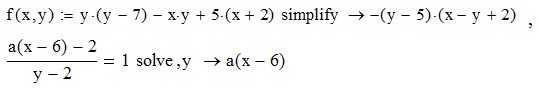Список литературы
- Задания № 20 ЕГЭ – 2015 [Электронный ресурс] // Материалы для подготовки к ЕГЭ и ГИА по математике. – Режим доступа: http://alexlarin.net/ege15.html.
- Плис, А. И. MATHCAD математический практикум [Текст] / А. И. Плис, Н. А. Сливина. – Финансы и статистика. – Москва, 2003. – 656 с.