ФОРМИРОВАНИЕ НАВЫКОВ РАБОТЫ С ФОРМУЛАМИ НА УРОКАХ ФИЗИКИ
Раздел: Проблемы и перспективы современного образования в предметных областях «Физика» и «Технология»
Журнал: Материалы III Международной очно-заочной научно-практической конференции. Часть 1
27 марта 2019 г.
Авторы: Степанов Анатолий Петрович
УДК 373.5.016:53
А. П. Степанов
A. P. Stepanov
Степанов Анатолий Петрович, учитель физики, МБОУ СОШ № 10, г. Юрга, Кемеровская область.
Stepanov Anatoliy Petrovich, teacher of phisics MBOU SOSH № 10, Jurga, Kemerovo region.
ФОРМИРОВАНИЕ НАВЫКОВ РАБОТЫ С ФОРМУЛАМИ НА УРОКАХ ФИЗИКИ
FORMATION OF SKILLS OF WORKING WITH FORMULAS IN PHYSICS LESSONS
Аннотация. Статья посвящена проблеме формирования одному из познавательных универсальных учебных действий школьников в процессе обучения физики – математическим преобразованиям формул. Приводится прием работы с формулами, который учащиеся легко усваивают и успешно применяют при решении задач. Развитие навыка работы с формулами повышает уровень усвоения курса физики и навыков решения задач, повышает интерес к изучению физики.
Annotation. The article is devoted to the problem of formation of cognitive universal educational actions of schoolchildren in the process of learning physics. The method of working with formulas is given, which students easily learn and successfully apply in solving problems. The development of the skill of working with formulas increases the level of mastering the course physics and problem solving skills, increases the interest in the study of physics.
Ключевые слова: познавательные универсальные учебные действия, анализ формул, математические преобразования формул.
Keywords: cognitive universal educational activities, formula analysis, mathematical transformations of formulas.
В процессе обучения учащихся физике и подготовке к ОГЭ и ЕГЭ приходится обучать школьников способам получения знаний, уделять внимание всем формам анализа – учебным текстам, графикам, таблицам, чертежам, формулам и т.п. При этом одной из наиболее важных и трудных задач является работа с формулами. Это связано с тем, что абстрактно-логическое мышление в этом возрасте развито недостаточно, а преобладает наглядно-образное. Трудность у учеников вызывает не только запомнить формулу, записать формулы, но и математические преобразования с формулами.
При работе с формулами ученик производит преобразование информации из символьной формы в словесную и наоборот. Качество операций мышления у учеников разное, что и сказывается на уровне понимания и запоминания материала. Для получения информации из готовой формулы необходимо произвести ее анализ, который может состоять, например, из ответов на поставленные вопросы:
- Как называется формула?
- Какие физические величины она связывает?
- Какой вид математической зависимости?
- Какой физический смысл представленной закономерности?
- Есть ли в формуле постоянные коэффициенты?
- Каков физический смысл постоянных коэффициентов?
- Какие производные формулы можно получить?
- Границы применимости формулы?
Обучение подобному анализу необходимо производить с первого года обучения физике.
При решении задач по физике требуется из формулы выразить неизвестную величину, следующим шагом необходимо подставить численные значения и получить ответ.
При этом необходимо объяснить учащимся, что лучше не решать физическую задачу по шагам: найти из одной формулы значение физической величины, затем подставлять ее во вторую формулу. Почему? Во-первых, получается неточный результат в вычислениях после многократного округления. Во-вторых, многие задачи невозможно решить таким путем, из-за того, что нет значения некоторой физической величины. Но решение проблемы часто заключается в том, что если бы мы подставили в буквенном виде одну формулу в другую, то эта неизвестная физическая величина сократилась бы.
Поэтому необходимо научить учащихся выражать из формулы необходимую физическую величину и преобразовывать формулы.
Часто встречающейся ошибкой учащихся является привычка подставлять числовые данные в формулу, получить простейшее уравнение в числах и из него уже выражать неизвестную величину. Этот прием позволяет решать только простейшие задачи и не может считаться полезным приемом работы с формулами.
В математике имеется набор правил при работе с формулами [1]. Рассмотрим уравнение A = b + c. Из этого уравнения нужно выразить величину b. Прибавим противоположный член (‒с) к обеим частям равенства, получим:
Однако в физике подобных преобразований принято не делать и сразу писать искомую величину. Это вызывает определенные трудности у учащихся. Для преодоления затруднений можно предложить следующее мнемоническое правило:
«При переносе величины через знак равенства арифметическая операция изменяется на противоположную».
Справедливость этого правила легко заметить, если рассмотреть рассмотренные выше математические преобразования.
Однако у некоторых учеников запоминание и применение этого правила вызывает затруднения, поэтому можно предложить следующий прием.
Рассмотрим отношение: 
.
Величину а будем считать стоящей вверху (в числителе), а величину b - стоящей внизу (в знаменателе). Тогда можно сформулировать следующие наглядные правила:
Правило № 1: Если величина стоит вверху, то при переносе через знак равенства она идет вниз (рис. 1).
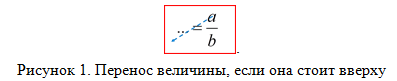
Правило № 2: Если величина стоит внизу, то при переносе через знак равенства она идет вверх (рис. 2).
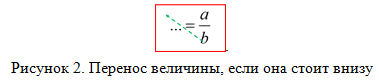
Правило № 3: Если величина со знаком плюс, то при переносе через знак равенства она будет со знаком минус (рис. 3).
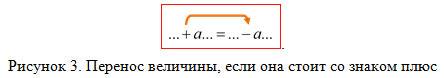
Правило № 4: Если величина со знаком минус, то при переносе через знак равенства она будет со знаком плюс (рис. 4).
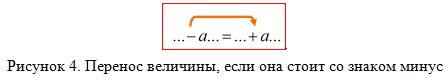
Как пользоваться этими правилами? Например, имеется формула 
. Необходимо выразить b. Величины c и d стоят вверху, значит, пойдут вниз. Величины e и f стоят внизу, значит пойдут вверх. Переставляя местами левую и правую части равенства, окончательно получим:
Практика показала, что данные правила легко усваиваются учениками и позволяют им без ошибок выражать неизвестную величину из формулы. При этом необходимо, чтобы учащиеся понимали, что в математике нет математической операции «перенос через знак равенства» и данные правилами являются полезными мнемоническими приемами, которые полезно знать и применять.
Учащиеся легко усваивают данную методику работы с формулами и успешно применяют ее при решении задач. Развитие этого навыка повышает уровень усвоения курса физики и навыков решения задач, при этом повышается интерес к изучению физики. Развитие умения работать с формулами способствует успешной сдачи ОГЭ и ЕГЭ.
Список литературы
- Болтянский В. Г. Лекции и задачи по элементарной математике [Текст]. / В. Г. Болтянский, Ю. В. Сидоров, М. И. Шабунин. – М. : Наука, 1974. – 576 с.