АНАЛИЗ И РАЗБОР ТИПИЧНЫХ ОШИБОК ЗАДАНИЙ ЕДИНОГО ГОСУДАРСТВЕННОГО ЭКЗАМЕНА ПО ТЕМЕ: «ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ»
Раздел: Проблемы и перспективы современного математического образования
Журнал: Материалы III Международной очно-заочной научно-практической конференции. Часть 1
27 марта 2019 г.
Авторы: Таллерова Анастасия Валерьевна
УДК 512:371.279.6
А. В. Таллерова
A. V. Tallerova
Таллерова Анастасия Валерьевна, студентка 2 курса магистратуры ФФМиТО УлГПУ, г. Ульяновск.
Tallerova Anastasiya Valerievna, 2-year student of a master’s degree of the faculty of physics, mathematics and technology education of ULSPU, Ulyanovsk.
АНАЛИЗ И РАЗБОР ТИПИЧНЫХ ОШИБОК ЗАДАНИЙ ЕДИНОГО ГОСУДАРСТВЕННОГО ЭКЗАМЕНА ПО ТЕМЕ: «ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ»
ANALYSIS AND PARSING OF TYPICAL ERRORS OF THE JOBS OF THE SINGLE STATE EXAM ON THE TOPIC: «LOGARIFMIC EQUATIONS»
Аннотация. Статья посвящена анализу и разбору типичных ошибок заданий единого государственного экзамена по математике профильного уровня на примере разбора логарифмических уравнений. Приводятся примеры заданий за выбранные периоды, и рассматриваются типичные ошибки учащихся, допускаемых при решении логарифмических уравнений.
Annotation. The article is devoted to the analysis of typical errors of tasks of the unified state exam in mathematics of the profile level on the example of the analysis of logarithmic equations. Examples of assignments for the selected periods are given, and typical student mistakes made when solving logarithmic equations.
Ключевые слова: логарифмы, свойства логарифмов, уравнения, типичные ошибки.
Keywords: logarithms, properties of logarithms, equation, typical error.
Одной из важных тем в курсе алгебры в средней школе является тема «Логарифмы». Тема очень непросто дается учащимся из-за подачи многообразия материала. Однако овладеть методикой решения логарифмических уравнений очень важно, так как повышаются умственные и творческие способности обучающихся, приобретаются навыки исследовательской работы, развиваются способности к логическому мышлению, происходит более глубокое усвоение учебного материала. Но более важным фактором является присутствие логарифмов в заданиях ЕГЭ.
В настоящее время учителю необходимо непрерывно повышать свой профессиональный уровень. Если раньше, до появления ЕГЭ, учитель считал, что подготовка выпускников к поступлению в вуз не является его главной задачей и он не несет ответственности за поступление учащихся в вуз, то сейчас каждый учитель должен быть заинтересован в получении высоких результатов ЕГЭ, так как по ним судят о его профессиональном уровне.
Чтобы обучающиеся смогли успешно сдать ЕГЭ, необходимо постоянно уделять внимание решению логарифмических уравнений на уроках. Главной задачей при изучении данной темы на уроках заинтересовать их темой. Но порою незнание определений, свойств, видов и способов решения, невнимательность, ведущая к допуску типичных ошибок, затрудняют деятельность учащихся. И для того, чтобы это предотвратить, необходимо проводить анализ заданий, разбор типичных ошибок.
Логарифмические уравнения в заданиях ЕГЭ профильного уровня встречаются в 5 и 13 заданиях. Заданием 5 являются уравнения, не требующие развёрнутого решения, по сравнению с заданием 13. Заданием № 13 являются уравнения, как правило, требующее замены переменной [1], позволяющей свести уравнение к квадратному, отбора корней на заданном отрезке, обусловленного ограниченностью новой переменной, наличием выражений с переменной под знаками логарифмов.
Проведя небольшой анализ 13 задания из ЕГЭ за период с 2011 по 2018 год можно сделать вывод. Во-первых, для решения логарифмических уравнений помимо определения логарифма и его свойств, ещё необходимо знать и уметь правильно и без ошибок решать другие виды уравнений, получаемые путём преобразований: квадратные, показательные, тригонометрические. Помимо этого, также немаловажную роль играет умение работать над алгебраическими выражениями, над их преобразованиями: группировка, вынесение общего множителя за скобки, применение формул сокращенного умножения и т.д.
Например, в одном из вариантов за 2017 год было представлено уравнение вида: ![]() . При решении данного логарифмического уравнения по определению логарифма, в результате задача свелась к решению тригонометрического уравнения
. При решении данного логарифмического уравнения по определению логарифма, в результате задача свелась к решению тригонометрического уравнения ![]() .
.
Во-вторых, задание № 13 варианта ЕГЭ часто представляет собой уравнение, которое нужно не просто решить, но и выбрать корни уравнения, удовлетворяющие условию.
Так, один из вариантов 2017 года включал следующее задание:
- Решите уравнение
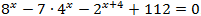 .
. - Укажите корни этого уравнения, принадлежащие отрезку
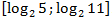 .
.
Также может попасться уравнение, которое сначала не будет подавать никаких признаков пребывания здесь логарифмов. Например, уравнение попавшееся учащимся в одном из вариантов за 2014 год, имело вид ![]()
При решении, путём алгебраических преобразований и вводом новой переменной, в итоге мы получаем два показательных уравнения 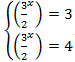 , решая которые получаются корни
, решая которые получаются корни 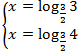 .
.
Поэтому для того, чтобы довести данное уравнение до конца, необходимо знать неразрывную связь между показательной и логарифмической функциями.
В-третьих, изучение методов решения логарифмических уравнений является хорошей подготовкой к решению задачи под номером 15, так как в основных методах решения и уравнений, и неравенств фактически используются одни и те же математические идеи.
Просматривая и анализируя задания из ЕГЭ за данные периоды, можно сделать вывод, что логарифмические уравнения не сдают своих позиций и остаются одной из важных и значимых тем, хоть и уступают тригонометрическим уравнениям.
Основные методы решения логарифмических уравнений несложно запомнить, их всего пять: сведение к простейшему уравнению, использование равносильных переходов, введение новых неизвестных, логарифмирование и разложение на множители. Как правило, в задаче № 13 встречаются уравнения, требующие применения перечисленных выше пяти основных методов.
Несмотря на то, что 13 задание достаточно традиционно, процент его выполнения всего 23 %, из которых один балл получают лишь 6 % школьников. Экзаменаторы отмечают, что ученики не понимают условие задания, допускают простейшие арифметические ошибки и не умеют себя проверить – все это, естественно, очень негативно влияет на результат [3].
Какие типичные ошибки совершают экзаменуемые? По-прежнему учащиеся теряют балл в 13 задании в пункте б) по причине отсутствия обоснованного отбора корней из промежутка.
Также при решении логарифмических уравнений следует обратить внимание учащихся на то, что применение следующих формул: ![]() может привести как к приобретению, так и к потере корней. При решении уравнений, заменяя выражение
может привести как к приобретению, так и к потере корней. При решении уравнений, заменяя выражение ![]() на выражение
на выражение ![]() , можно получить посторонние корни. А вот потеря корней происходит при делении обеих частей уравнения на одно и то же выражение, содержащее неизвестное. Поэтому рекомендуется следить за равносильностью уравнений [1], получаемых в результате преобразований.
, можно получить посторонние корни. А вот потеря корней происходит при делении обеих частей уравнения на одно и то же выражение, содержащее неизвестное. Поэтому рекомендуется следить за равносильностью уравнений [1], получаемых в результате преобразований.
Еще одна ошибка – применение свойств логарифмов без учета области допустимых значений. Например, хорошо знакомое многим свойство «логарифм произведения равен сумме логарифмов», оказывается, имеет уточнение: ![]() Действительно, для того, чтобы было определено выражение в левой части этого равенства, достаточно, чтобы произведение функций f и g было положительным, но сами функции при этом могут быть как одновременно больше, так и одновременно меньше нуля, поэтому при применении данного свойства необходимо использовать понятие модуля [2].
Действительно, для того, чтобы было определено выражение в левой части этого равенства, достаточно, чтобы произведение функций f и g было положительным, но сами функции при этом могут быть как одновременно больше, так и одновременно меньше нуля, поэтому при применении данного свойства необходимо использовать понятие модуля [2].
И таких примеров можно привести немало. Поэтому для эффективного освоения решения логарифмических уравнений необходимо не только прорешивать подобные задания самостоятельно, но и также обращаться за помощью к опытным преподавателям, которые расскажут обо всех «подводных камнях».
Список литературы
- Шестаков, С. А. ЕГЭ 2011. Математика. Задача С1. Уравнения и системы уравнений [Текст] / С. А. Шестаков, П. И. Захаров : под ред. А. Л. Семенова и И. В. Ященко. – М. : МЦНМО, 2011. – 120 с.
- Тишин, В. И. Логарифмические уравнения. Методическое пособие для средней школы [Текст]. / В. И. Тишин. – Брянск, 2002. – 45 с.
- Далингер, В. А. Причины типичных ошибок, допускаемых учащимися в процессе изучения математики и самоконтроль как средство организации рефлексии по предупреждению ошибок / В. А. Далингер, О. А. Тарасова : под ред. О. И. Кирикова. – Кн. 2. – Воронеж : ВГПУ, 2004. – С. 216-143.
