СИСТЕМА РАБОТЫ УЧИТЕЛЯ МАТЕМАТИКИ ПО РАЗВИТИЮ СМЫСЛОВОГО ЧТЕНИЯ В ХОДЕ ОБУЧЕНИЯ РЕШЕНИЮ ТЕКСТОВЫХ ЗАДАЧ
Раздел: Проблемы и перспективы современного математического образования
Журнал: Материалы III Международной очно-заочной научно-практической конференции. Часть 1
27 марта 2019 г.
Авторы: Пидоря Татьяна Александровна
УДК 373.5.016:51
Т. А. Пидоря
Т. А. Pidorya
Пидоря Татьяна Александровна, учитель математики, Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа № 6», г. Верхняя Салда, Свердловская область.
Pidorya Tatiana Alexandrovna, teacher of Mathematics, Secondary comprehensive school № 6, Upper Salda, Sverdlovsk region.
СИСТЕМА РАБОТЫ УЧИТЕЛЯ МАТЕМАТИКИ ПО РАЗВИТИЮ СМЫСЛОВОГО ЧТЕНИЯ В ХОДЕ ОБУЧЕНИЯ РЕШЕНИЮ ТЕКСТОВЫХ ЗАДАЧ
SYSTEM OF WORK OF TEACHERS OF MATHEMATICS ON THE DEVELOPMENT OF SEMANTIC READING DURING TRAINING TO SOLVE THE TEXT TASKS
Аннотация. Статья посвящена формированию и развитию смыслового чтения в ходе обучения решению задач в курсе математики 5-6 классов и алгебры 7-9 классов. Приводится описание системы работы учителя по обучению решению задач при помощи табличного способа записи условия задачи и введения неизвестных. Рассматриваются различные примеры задач, позволяющие вырабатывать у обучающихся навыки работы с информацией.
Annotation. This article is dedicated to the problem of forming and developing the ability to understanding the mathematical problem quickly using the method of thematic reading in the course of Mathematics in 5-6 classes and in the course of Algebra in 7-9 classes. Here you can see the system of the work of a teacher, her methods of using special tables for putting down the content of the problem. Here you can see some examples of mathematical problems showing the ways of developing the ability to work with information.
Ключевые слова: познавательные универсальные учебные действия, смысловое чтение, решение задач, навык работы с текстом.
Keywords: cognitive universal educational activities, thematic reading, solve mathematical problems, text working skills.
Читать – это ещё ничего не значит;
что читать и как понимать читаемое –
вот в чём главное дело.
К. Д. Ушинский
Современный учитель – учитель, реализующий ФГОС ООО и готовый к реализации ФГОС СОО, ставящий перед собой цель дать качественное образование своим обучающимся. Качество образования в соответствии с федеральными государственными стандартами заключается в достижении нашими учениками высоких предметных, метапредметных, а также личностных результатов.
Вполне закономерно в Федеральных государственных образовательных стандартах общего образования [4], отражающих государственный, социальный и индивидуальный заказы, особо подчеркивается важность обучения школьников смысловому чтению. В них отмечается, что чтение в современном информационном обществе имеет метапредметный характер, а умения такого чтения относятся к универсальным учебным действиям. Следовательно, каждый предмет должен реализовать возможности для формирования и развития обозначенных умений (А. Г. Асмолов, Г. В. Бурменская, И. А. Володарская).
Смысловое чтение – вид чтения, которое нацелено на понимание читающим смыслового содержания текста [5]. Для смыслового понимания недостаточно просто прочесть текст, необходимо дать оценку информации, откликнуться на содержание. Составляющие смыслового чтения входят в структуру всех универсальных учебных действий:
- в личностные УУД – входят мотивация чтения, мотивы учения, отношение к себе и к школе;
- в регулятивные УУД – принятие учеником учебной задачи, произвольная регуляция деятельности;
- в познавательные УУД – логическое и абстрактное мышление, оперативная память, творческое воображение, концентрация внимания, объем словаря;
- в коммуникативные УУД – умение организовать и осуществить сотрудничество и кооперацию с учителем и сверстниками, адекватно передавать информацию, отображать предметное содержание и условия деятельности в речи.
Особое значение в формировании универсального действия смыслового чтения имеют предметы математического цикла.
Представлю свою систему работы по обучению решения задач при помощи таблиц, в которых излагается краткая запись условия задачи, вводятся неизвестные. Основные особенности предлагаемого подхода связаны с тем, что главная задача сфокусирована на тщательном прочтении предлагаемого текста. Чтобы чтение стало осмысленным, необходимо чтобы оно сопровождалось дополнительным заданием, например, выбором ключевых слов, поэтапным заполнением таблицы. Данные приёмы развивают в ученике навык работы с письменным текстом, учат анализировать данные, логически структурировать информацию, выбирать главное, а также повышают качество учебной деятельности в целом.
План работы по решению задачи:
1. Первое чтение, после которого отвечаем на вопросы:
- Кто «действующие лица и исполнители»?
- Какие ключевые слова мы выделим для решения задачи?
2. Рисуем карандашом и линейкой таблицу, чаще всего 3х4. Вписываем данные первого чтения.
3. Второе чтение. Что необходимо найти? Определяем главный вопрос в задаче. Ставим вопросительный знак в нужной клетке таблицы.
4. Третье чтение. Осмысленное. Выбираем данные задачи по каждому «исполнителю» и ключевому слову. Если не получается с первого раза повторяем чтение текста задачи. При необходимости второе и третье чтение можно менять местами либо объединить.
5. Если арифметическая задача, то определяем порядок действий, составляем план решения. Если задачу будем решать при помощи составления уравнения, то вводим неизвестное, заполняем все клетки таблицы и по последнему заполненному столбцу составляем уравнение.
6. Решение по действиям или решение уравнения.
7. Запись ответа. Проверка существования полученного ответа.
Приведу отдельные примеры по обучению решения задач при помощи таблиц.
5 класс. Тема «Формулы» (по учебнику Н. Я. Виленкина).
№ 680. С одной станции в противоположных направлениях вышли два поезда в одно и тоже время. Скорость одного поезда 50 км/ч, а скорость другого поезда 70 км/ч. Какое расстояние будет между ними через t часов после выезда? Запишите ответ в виде формулы и упростите ее. Какой смысл имеет число 120 в получившейся формуле? [3] (табл. 1).

Чертим таблицу (табл. 2).
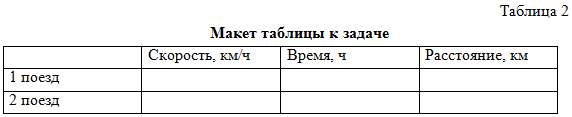
Ключевые слова, характеристики движения записываем сразу с указанием единиц измерения.
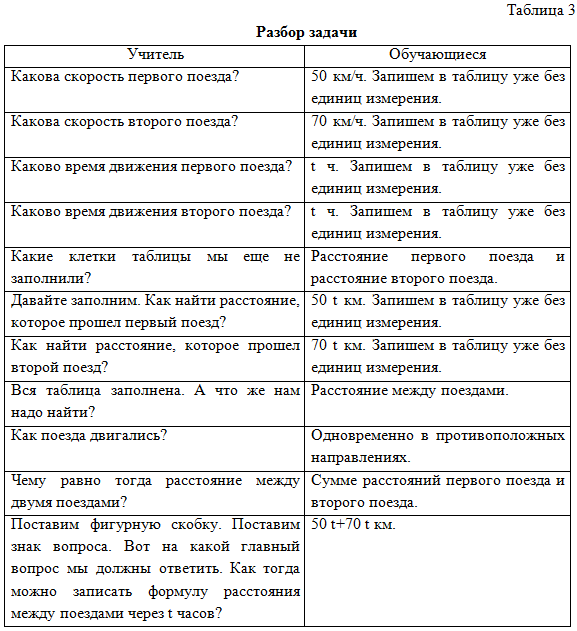
Второе и третье чтение задачи. Параллельное заполнение таблицы 3.
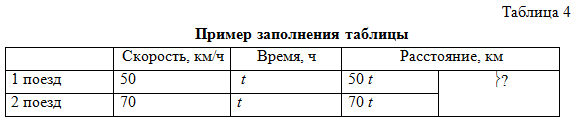
В тетради у обучающихся таблица выглядит так, как показано в таблице 4.
Далее обучающиеся решают задачу (табл. 5).
50 t+70 t= 120t (км/ч) – расстояние между поездами через t часов.
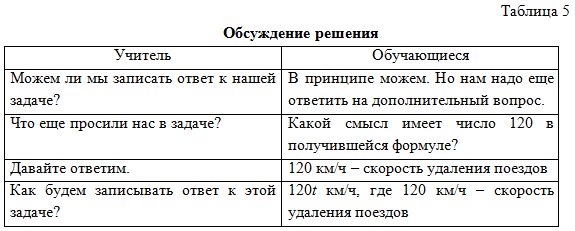
Задача решена. Обучающиеся записали ответ. Мною обязательно повторяются этапы решения задачи, одновременно интересуясь у учащихся, что осталось для них непонятым.
Для меня важно закрепить понимание подхода к решению задач при помощи составления таблицы, и поэтому далее вызываю одного ученика для решения задачи № 681. Задача аналогичная, но на скорость сближения. Для закрепления изученного дома предлагаю решить задачу № 683.
Табличный способ решения отрабатывается мною на задачах, решаемых с помощью уравнения. Разбираю не только задачи на движение, но и другие задачи, в которых выделяются три характеристики описываемых явлений (было, взяли/положили, осталось/стало; в задачах на работу: производительность труда; время, затраченное на выполнение работы; объем выполненной работы; в задачах на приобретение: цена товара, количество товара, стоимость товара и т.д.).
Так при объяснении темы «Решение задач с помощью уравнений» (по учебнику Ю. Н. Макарычева) на примере задачи 1 сразу показываю учащимся табличный способ оформления условия задачи (табл. 6), который в учебнике не показан.
Задача 1. В корзине было в 2 раза меньше яблок, чем в ящике, После того как из корзины переложили в ящик 10 яблок, в ящике их стало в 5 раз больше, чем в корзине. Сколько яблок было в корзине и сколько в ящике? [1]
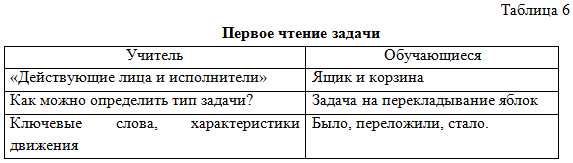
В данном случае обязательно обращаю внимание на ключевое слово «переложили»: для корзины – взяли, убавили, для ящика – добавили, положили. Одно слово описывает двойной процесс.
Чертим таблицу (табл. 7). Второе и третье чтение задачи позволяют заполнить ключевые слова, характеристики действий с ящиком и корзиной сразу с указанием единиц измерения, записать все данные задачи в таблицу 7.

Далее всегда обращаю внимание на введение неизвестных и по последнему заполненному столбику в таблице учу составлять уравнение и решать задачу.
7 класс. Тема «Решение задач с помощью систем уравнений» (по учебнику Ю. Н. Макарычева).
№ 1107. Два автомата изготавливают детали. Число деталей, изготовленных первым автоматом за 3 часа и вторым за 2 часа, составляет 730 штук. Четвертая часть деталей, изготовленных обоими автоматами за 2 часа, составляет 150 штук. Сколько деталей изготовлял каждый автомат за час? [1].
Чертим таблицу (табл. 8).

Второе и третье чтение задачи позволяют заполнить ключевые слова, характеристики действий с указанием единиц измерения, записать все данные задачи в таблицу 8. При заполнении таблицы привожу учащихся к пониманию, что здесь описаны 2 ситуации, а, значит, придется составить 2 таблицы и соответственно 2 уравнения, которые затем необходимо решить совместно.
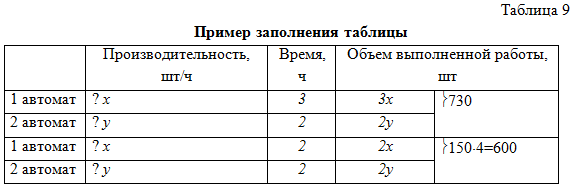
Обращая внимание на введение неизвестных и по последним заполненным столбикам в таблице, учу составлять систему уравнений и далее решать задачу.
8 класс. Тема «Решение задач с помощью квадратных уравнений» (по учебнику Ю. Н. Макарычева).
№ 568. В кинотеатре число мест в ряду на 8 больше числа рядов. Сколько рядов в кинотеатре, если всего в нем имеется 884 места? [2].
Чертим таблицу 10.

Второе и третье чтение задачи позволяют заполнить ключевые слова, записать все данные задачи в таблицу 11. При заполнении таблицы привожу учащихся к пониманию, что здесь описана всего 1 ситуация, а, значит, составляем соответственно 1 уравнение, которое является квадратным.

Необходимо обращать внимание на введение неизвестных и, особенно, на их область допустимых значений. В данном случае: х![]() N. Это помогает учащимся в конце своего решения выполнить проверку полученных значений с точки зрения смысла задачи. Учу составлять квадратное уравнение по последнему заполненному столбику в таблице и далее решать задачу, соблюдая все этапы ее решения.
N. Это помогает учащимся в конце своего решения выполнить проверку полученных значений с точки зрения смысла задачи. Учу составлять квадратное уравнение по последнему заполненному столбику в таблице и далее решать задачу, соблюдая все этапы ее решения.
Такой же подход использую при объяснении темы «Решение задач с помощью рациональных уравнений» (п. 26 учебника).
Задача 1. Моторная лодка прошла 25 км по течению реки и 3 км против течения, затратив на весь путь 2 ч. Какова скорость лодки в стоячей воде, если скорость течения реки равна 3 км/ч? [2].
Чертим таблицу 12.
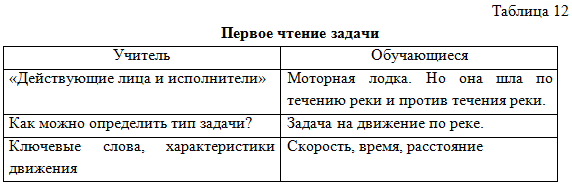
Таблица при решении задачи учащимися заполняется при втором и третьем чтении (табл. 13).

Здесь обязательно обращаю внимание на введение неизвестных и на их область допустимых значений. Это позволяет затем легче учащимся понять и выполнить проверку полученных значений с точки зрения смысла задачи. Потому при решении задач на движение по реке обычно рекомендую выполнить дополнительную строчку для записи скорости моторной лодки в стоячей воде. Учу составлять рациональное уравнение по последнему заполненному столбику в таблице и далее решать задачу, соблюдая все этапы ее решения.
Трудность у учащихся вызывают задачи на совместную работу. Табличный способ оформления условия задачи и переход к решению уравнения превращает эти задачи в обычные, нивелирует всю трудность задачи. Покажу только заполненную по условию задачи таблицу, из которой сразу видно уравнение, и только дело техники дальнейшее решение задачи.
№ 632. При совместной работе двух кранов разгрузку баржи закончили за 6 часов. Сколько времени потребовалось бы каждому крану отдельно для разгрузки баржи, если известно, что первому крану для этого требуется на 5 часов больше, чем второму? [2].
Чертим таблицу 14.
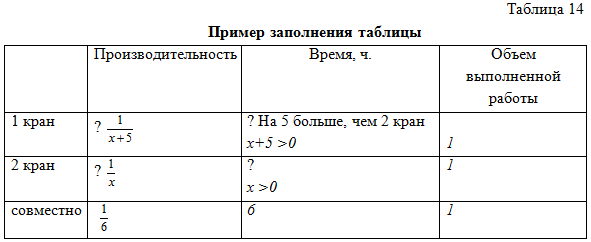
При обучении решению задач необходимо всегда прибегать к математическому творчеству учащихся как к высшей форме самостоятельности их мышления [7]. «Математический опыт учащегося нельзя считать полным, если он не имел случая решить задачу, изобретенную им самим», – говорил Д. Пойа. Именно поэтому прошу ребят составить свои задачи по изучаемой теме. Самостоятельное написание текста математической задачи и смысловое чтение составленной кем-то задачи – это некая двойственность в математике и математических упражнениях. Но именно самостоятельное составление математических задач позволяет учащимся задуматься о значимости каждого используемого слова в тексте задачи, о достаточности данных в задаче, о подборе ключевых слов, а, следовательно, ведет к развитию смыслового чтения у обучающихся.
Таким образом, система работы по обучению решения задач табличным способом записи их условий достаточно эффективна с точки зрения достижения планируемых как предметных, так и метапредметных результатов образования обучающихся. Достижению этих результатов способствует смысловое чтение предлагаемого текста задачи.
Научить школьника приёмам работы с учебником, с книгой – это значит научить его учиться [6]. Важно научить ученика самостоятельно работать с книгой, вырабатывать умения и навыки осмысленного чтения и осознанного усвоения изложенного в ней материала. Рассмотренные приёмы работы с текстом учебника обеспечивают не только усвоение учебного материала, но и активизирует умственную деятельность учащихся, прививает интерес к изучаемому предмету.
Список литературы
- Макарычев, Ю. Н. Алгебра. 7 класс. : учеб. для общеобразоват. организаций [Текст]. / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. В. Суворова. // под ред. С. А. Теляковского. – 6-е изд. – М. : Просвещение,2016. – 256 с. : ил.
- Макарычев, Ю. Н. Алгебра. 8 класс: учеб. для общеобразоват. учреждений [Текст]. / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. // под ред. Теляковского. – 17-е изд. – М. : Просвещение, 2009. – 271 с. : ил.
- Виленкин, Н. Я. Математика. 5 класс: учеб. Для учащихся общеобразоват. организаций [Текст]. / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. – 34-е изд., стер. – М. : Мнемозина, 2015. – 280 с. : ил.
- Федеральные государственные образовательные стандарты [Электронный ресурс]. – Режим доступа : https://fgos.ru/
- Понятие смыслового чтения [Электронный ресурс]. – Режим доступа : https://sites.google.com/site/ucitelamv/home/cto-takoe-smyslovoe-ctenie
- Береснева, Г. Б. Приёмы работы с учебником на уроках математики. [Электронный ресурс]. / Г. Б. Береснева. – Режим доступа : https://nsportal.ru/shkola/algebra/library/2012/11/05/priyomy-raboty-s-uchebnikom-na-urokakh-matematiki
- Петракова, Н. П. Математическое творчество – высшая форма самостоятельности мышления учащихся [Электронный ресурс]. / Н. П. Петракова. // Научно-методический электронный журнал «Концепт». – 2015. – Т. 6. – С. 111–115. –Режим доступа : http://e-koncept.ru/2015/65223.htm.
