ИССЛЕДОВАНИЕ ФУНКЦИЙ В КУРСЕ АЛГЕБРЫ ОСНОВНОЙ ШКОЛЫ С ИСПОЛЬЗОВАНИЕМ ДИНАМИЧЕСКИХ МАТЕМАТИЧЕСКИХ ПРОГРАММ
Раздел: Проблемы и перспективы современного математического образования
Журнал: Материалы III Международной очно-заочной научно-практической конференции. Часть 1
27 марта 2019 г.
Авторы: Фомина Анжелла Владимировна , Князева Екатерина Алексеевна
УДК 373.5.016:512
Е. А. Князева, А. В. Фомина
E. A. Knyazeva, A. V. Fomina
Князева Екатерина Алексеевна, студентка 5 курса ФИМЭ, НФИ КемГУ, г. Новокузнецк.
Фомина Анжелла Владимировна, к. физ.-мат. н., доцент, НФИ КемГУ, г. Новокузнецк.
Knyazeva Ekaterina Alekseevna, 5-year student; Fomina Anzhella Vladimirovna, candidate of physical and mathematical Sciences, associate Professor, Novokuznetsk Institute (branch) «Kemerovo State University», Novokuznetsk.
ИССЛЕДОВАНИЕ ФУНКЦИЙ В КУРСЕ АЛГЕБРЫ ОСНОВНОЙ ШКОЛЫ С ИСПОЛЬЗОВАНИЕМ ДИНАМИЧЕСКИХ МАТЕМАТИЧЕСКИХ ПРОГРАММ
THE STUDY OF FUNCTIONS IN ALGEBRA COURSE OF THE PRIMARY SCHOOL WITH THE USE OF DYNAMIC MATHEMATICAL SOFTWARE
Аннотация. Статья посвящена проблеме использования динамических математических программ в процессе изучения функций. Приводятся примеры заданий, решенных с помощью программы GeoGebra.
Annotation. The article is devoted to the problem of using dynamic mathematical programs in the process of studying functions. Examples of tasks solved using the GeoGebra program are given.
Ключевые слова: исследование функций, квадратичная функция, задания на нахождение области определения, система динамической геометрии.
Keywords: research of functions, quadratic function, tasks on finding the domain of definition, system of dynamic geometry.
Федеральный государственный образовательный стандарт среднего общего образования, утвержденный приказом Минобразования науки России от 17 апреля 2012 года № 413, предъявляет к результатам обучения курса алгебры и начал математического анализа, геометрии новые требования, связанные с овладением приемами использования компьютерных программ. Введение ФГОС нового поколения в учебный план способствует оптимизации учебного процесса, разнообразию форм проведения урока, формированию интереса учащихся к математике, кроме того обучение математике по информационно-технологической траектории для подрастающего поколения является ключом к реализации созревающих профильных интересов учащихся, их самовыражению в учении и творческой активности. Именно здесь учащимся предлагаются разнообразные траектории дополнительного изучения предмета в рамках профильных курсов, факультативов, клубной и проектной деятельности в области информатики [1].
Понятие функции является абстрактным и достаточно сложным для восприятия учащимися. Следовательно, основная задача учителя состоит в том, чтобы сделать изучение сложного учебного материала максимально наглядным и понятным. На наш взгляд, одним из путей решения данной задачи является использование динамических математических программ. К ним относятся системы динамической геометрии, которые позволяют изменить традиционные подходы к изучению функций и их свойств, используя такие дидактические возможности систем как наглядность, моделирование и динамика.
Визуализация учебной информации при изучении функциональной линии с использованием средств ИКТ, к которым относятся также системы динамической геометрии, заключается не столько в демонстрации образа изучаемого объекта, сколько в создании, конструировании этого образа и дальнейшем его исследовании. Статическое изображение является частным видом функции с заданными числовыми коэффициентами, а динамическое изображение представляет собой семейство функций, позволяющее установить зависимость изучаемого объекта от определяющих его коэффициентов или параметров. Выводы, сделанные с использованием статического чертежа, не всегда являются убедительными, так как зависимость свойств рассматриваемых функций не всегда явно прослеживается и остается, в основном, скрытой для учащихся, поэтому выводы лучше выполнять с использованием динамических чертежей. Динамические чертежи возможно построить, например, с помощью программ «Живая математика» и GeoGebra.
GeoGebra является динамическим программным обеспечением и геометрической средой, предназначенной для построения различных фигур, начиная от простейших парабол, эллипсов и заканчивая пространственными 3D-моделями. Сочетание алгебраического, геометрического и числового анализа дает возможность создавать конструкции с точками, линиями, векторами, математическими функциями с возможностью их дальнейшего изменения, то есть полученными объектами учащиеся могут легко манипулировать на плоскости и в пространстве [2].
Рассмотрим и решим задачу по теме «Квадратичная функция» в среде GeoGebra. Сначала решим задачу аналитическим способом и проверим правильность графическим.
1. Определите область значения функции y = 3x² - 6x + 1.
Аналитическое решение: коэффициент при x² положительный, область значений функции вычисляется по формуле:
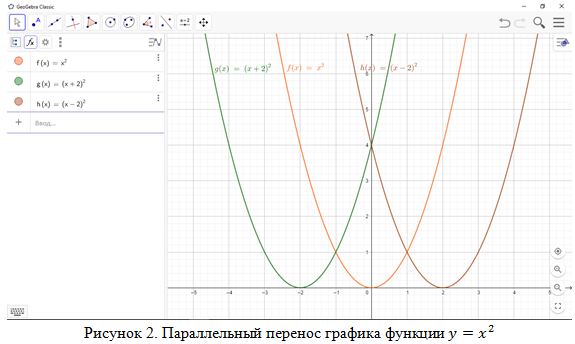
При помощи этой программы также можно наглядно выполнять преобразования графиков: параллельный перенос, отображение, деформацию (сжатие и растяжение), отражение. Например, выполним параллельный перенос графика функции с использованием программы GeoGebra.
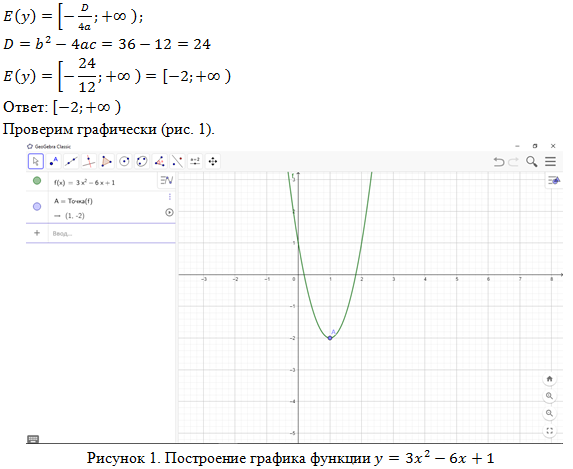
График функции y = f (x + b) получается параллельным переносом графика функции y = f (x) в положительном направлении вдоль оси Ox на расстояние b, если b < 0 и в отрицательном направлении вдоль оси Ox, если b > 0 (рис. 2).
Динамическая среда GeoGebra может применяться учителями не только для объяснения темы «Квадратичная функция», но и для многих других тем при изучении функций и построении их графиков в основной школе. GeoGebra повышает интерес учащихся к изучаемой теме, их понимание данной темы, а также внимание учеников на уроке. Данная программа может использоваться для решения задач на интерактивной доске или в компьютерном классе.
Список литературы
- Федеральный государственный образовательный стандарт среднего общего образования [Текст] : утвержден приказом Министерства образования и науки РФ от 17 мая 2012 г. N 413/ Министерство образования и науки Российской Федерации. – М. – 2012.
- Андрафанова, Н. В. Применение компьютерных технологий при изучении функциональной линии в школьном курсе математики [Электронный ресурс] / Н. В. Андрафанова, К. И. Суханова // Наука вчера, сегодня, завтра. – 2011. – № 5 – С. 76-82. – Режим доступа : https://sibac.info/conf/science/xxxiv/53410.
