РЕШЕНИЕ ЗАДАЧ ЕГЭ С ИСПОЛЬЗОВАНИЕМ АЛГОРИТМОВ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
Раздел: Профессиональное образование и технологическое обучение в РФ и за рубежом
Журнал: Материалы XIV Международной научно-практической конференции
30 декабря 2019 г.
Авторы: Рябинина Елизавета Евгеньевна
УДК 004.42:371.26
Е. Е. Рябинина
E. E. Ryabinina
Рябинина Елизавета Евгеньевна, студентка 5 курса, ФИМЭ, НФИ КемГУ, г. Новокузнецк, Россия.
Научный руководитель: Можаров Максим Сергеевич, канд. пед. наук, профессор, зав. кафедры ИОТД ФГБОУ ВО НФИ КемГУ, г. Новокузнецк, Россия.
Ryabinina Elizaveta Evgenievna, 5th year student, FIME, NFI KemSU, Novokuznetsk, Russia.
Scientific adviser: Mozharov Maksim Sergeevich, Candidate of Pedagogical Sciences, Professor, Head of the Department of Engineering and Technology, FSBEI HE NFI KemSU, Novokuznetsk, Russia.
РЕШЕНИЕ ЗАДАЧ ЕГЭ С ИСПОЛЬЗОВАНИЕМ АЛГОРИТМОВ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
SOLUTION OF USE EXAMPLES USING DYNAMIC PROGRAMMING ALGORITHMS
Аннотация. В статье приводится разбор 22 задания ЕГЭ по информатике на тему «Динамическое программирование» Формируемые при изучении приведенного в статье материала компетенции школьников позволят эффективно решать все типы заданий на данную тему. Основная сложность при решении данного задания у школьников заключается в невнимательном изучении условий поставленной задачи и неправильного выбора алгоритма её решения. Поэтому особую ценность, на наш взгляд, представляет адаптированный материал, приведенный в статье. В данной работе рассмотрены основные виды 22 задания, встречающиеся в ЕГЭ по информатике, и разобраны примеры по теме «Динамическое программирование».
Annotation. The article provides an analysis of 22 tasks of the exam in computer science on the topic «Dynamic Programming». The competencies of students formed in the study of the material cited in the article will effectively solve all types of tasks on this topic. The main difficulty in solving this task among students is inattentive study of the conditions of the task and the wrong choice of algorithm for solving it. Therefore, of particular value, in our opinion, is the adapted material given in the article. In this paper, we consider the main types of 22 tasks found in the exam in computer science and analyze examples on the topic «Dynamic Programming».
Ключевые слова: информатика, методика обучения информатике, динамическое программирование, ЕГЭ.
Keywords: computer science, methods of teaching computer science, dynamic programming, USE.
Согласно анализу результатов сдачи единого государственного экзамена по информатике прошлых лет 22 задание не вызывает особой сложности у школьников, хотя и считается задачей повышенного уровня сложности и приносит 1 первичный балл. На самом деле, при подготовке к решению заданий на «Динамическое программирование» необходимо запомнить основные алгоритмы решения и знать, когда их можно применить. Это и является главной проблемой у школьников при решении данного задания.
Что необходимо знать учащемуся при подготовке к решению данного задания:
- динамическое программирование – это способ решения сложных задач путем сведения их к более простым задачам того же типа
- с помощью динамического программирования решаются задачи, которые требуют полного перебор вариантов:
– «подсчитайте количество вариантов…»
– «как оптимально распределить…»
– «найдите оптимальный маршрут…» - динамическое программирование позволяет ускорить выполнение программы за счет использования дополнительной памяти; полный перебор не требуется, поскольку запоминаются решения всех задач с меньшими значениями параметров [3, с. 141].
Самый простейший пример реализации данного метода: определение последовательности чисел Фибоначчи: 1, 1, 2, 3, 5, 8 и т.д.
F1 =1, F2 =1, F3 = F1+ F2
Получаем рекуррентную формулу: Fn = Fn-2+ Fn-1.
Рекуррентная формула — формула, выражающая каждый член последовательности через p предыдущих членов [1, с. 52].
Задания ЕГЭ по данной теме можно разделить на разные категории: «количество программ с обязательным этапом», «поиск количества программ по заданному числу», «поиск количества чисел по заданному числу команд» Рассмотрим примеры решения заданий на тему «Динамическое программирование» различных типов.
Задание 1:
Исполнитель Май4 преобразует число, записанное на экране. У исполнителя три команды, которым присвоены номера:
1. прибавь 1
2. прибавь 2
3. прибавь 4
Первая из них увеличивает число на экране на 1, вторая увеличивает это число на 2, а третья – на 4. Программа для исполнителя Май4 – это последовательность команд. Сколько есть программ, которые число 21 преобразуют в число 30?
Решение:
- заметим, что при выполнении любой из команд число увеличивается (не может уменьшаться);
- все числа, меньшие начального числа 21, с помощью этого исполнителя получить нельзя, для них количество программ будет равно 0;
- для начального числа 21 количество программ равно 1: существует только одна пустая программа, не содержащая ни одной команды; если через
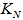обозначить количество разных программ для получения числа N из начального числа 21, то 
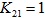; - теперь рассмотрим общий случай, чтобы построить рекуррентную формулу, связывающую 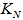с предыдущими элементами последовательности
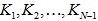, то есть с решениями таких же задач для меньших N; - любое число N > 21 могло быть получено одной из трёх операций сложения соответственно из чисел N-1, N-2 и N-4, поэтому
-
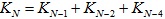; - остается по этой формуле заполнить таблицу для всех значений от 21 до 30:
Ответ: 96 [2].
Рассмотрим пример задачи, где необязательно использовать рекуррентную формулу и таблицу для решения. Для решения достаточно рассмотреть все возможные комбинации.
Задание 2:
У исполнителя Калькулятор две команды
1. умножь на 2
2. умножь на 3.
Первая из них умножает число на экране на 2, вторая – утраивает его. Сколько различных чисел можно получить из числа 2 с помощью программы, которая содержит ровно 3 команды?
Решение:
– С помощью одной команды из числа 2 можно получить два различных числа:
2 * 2 = 4
2 * 3 = 6.
– С помощью двух команд можно получить по два числа из 4 и 6:
4 * 2 = 8
4 * 3 = 12
6 * 2 = 12
6 * 3 = 18
Видим, что два результата совпадают, поэтому получилось 3 числа, а не 4.
– С помощью трёх команд получаются следующие числа.
12 * 2 = 24
12 * 3 = 36
8 * 2 = 16
8 * 3 = 24
18 * 2 = 36
18 * 3 = 54
Числа 36 и 24 встречаются дважды, поэтому всего получаем четыре различных числа.
Ответ: 4 [2].
Для решения задач по теме «Динамическое программирование» часто используют метод «от обратного». Рассмотрим задачу, где с помощью рекуррентной формулы и данного метода, приводится решение.
Задание 3:
Исполнитель Фибо преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 2
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 2. Программа для исполнителя Фибо – это последовательность команд.
Сколько существует программ, которые преобразуют исходное число 3 в число 20 и при этом траектория вычислений содержит число 9 и не содержит числа 15?
Траектория вычислений – это последовательность результатов выполнения всех команд программы. Например, для программы 212 при исходном числе 7 траектория будет состоять из чисел 9, 10, 12.
Решение:
Искомое количество программ равно произведению количества программ, получающих из числа 3 число 9, на количество программ, получающих из числа 9 число 14 и на количество программ, получающих из числа 16 число 20, поскольку траектория вычислений не должна содержать числа 15.
Пусть R(n) – количество программ, которые число 3 преобразуют в число n, P(n) – количество программ, которые число 9 преобразуют в число n, а F(n) – количество программ, которые преобразуют число 16 в число n.
Для всех n > 4 верны следующие соотношения:
1. R(n) = R(n − 1) + R(n − 2), так как существует два способа получения n – прибавлением единицы или прибавлением двойки. Аналогично P(n) = P(n − 1) + P(n − 2) и F(n) = F(n − 1) + F(n − 2).
– Последовательно вычислим значения R(n):
R(3) = 1.
R(4) = 1.
R(5) = R(3) + R(4) = 2.
R(6) = R(5) + R(4) = 3.
R(7) = R(6) + R(5) = 5.
R(8) = R(7) + R(6) = 8.
R(9) = R(8) + R(7) = 13.
– Теперь вычислим значения P(n):
P(9) = 1.
P(10) = 1.
P(11) = P(9) + P(10) = 2.
P(12) = P(10) + P(11) = 3.
P(13) = P(11) + P(12) = 5.
P(14) = P(12) + P(13) = 8.
– Теперь вычислим значения F(n):
F(16) = 1.
F(17) = 1.
F(18) = F(16) + F(17) = 2.
F(19) = F(17) + F(18) = 3.
F(20) = F(18) + F(19) = 5.
Таким образом, количество программ, удовлетворяющих условию задачи, равно 13 · 8 · 5 = 520.
Ответ: 520 [2].
Задание 4:
Исполнитель НечетМ преобразует число на экране. У исполнителя НечетМ две команды, которым присвоены номера:
1. прибавь 1
2. сделай нечётное.
Первая из этих команд увеличивает число x на экране на 1, вторая переводит число x в число 2x+1. Например, вторая команда переводит число 10 в число 21. Программа для исполнителя НечетМ – это последовательность команд. Сколько существует таких программ, которые число 1 преобразуют в число 27, причём траектория вычислений не содержит число 26? Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 17, 18.
Решение:
Используем метод динамического программирования. Заведем массив dp, где dp[i] – кол-во способов получить число i с помощью таких команд.
– База динамики:
dp[1]=1;
– Формула перехода:
dp[i]=dp[i-1] - если i - четное.
dp[i]=dp[i-1] + dp[(i-1)/2] - если i нечетное.
– Но при этом, если i-1 = 26 или (i-1)/2 = 26, то оно не учитывается. Можно заметить, что для числа 27 будет формула dp[27]=dp[26] + dp[13], а поскольку dp[26] не считается, то ответ совпадает с dp[13].
– Посчитаем dp[13] (далее будет приведены значения в ячейках dp от 1 до 13): 1 1 2 2 3 3 5 5 7 7 10 10 13.
Ответ: 13 [2].
Задание для самостоятельной подготовки:
1. Исполнитель Май17 преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Прибавить 3
Первая команда увеличивает число на экране на 1, вторая увеличивает его на 3. Программа для исполнителя Май17 – это последовательность команд.
Сколько существует программ, для которых при исходном числе 1 результатом является число 17 и при этом траектория вычислений содержит число 9? Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 11, 12 [3, с. 146].
2. Исполнитель НечетМ преобразует число на экране. У исполнителя НечетМ две команды, которым присвоены номера:
1. прибавь 1
2. сделай нечётное.
Первая из этих команд увеличивает число x на экране на 1, вторая переводит число x в число 2x+1. Например, вторая команда переводит число 10 в число 21. Программа для исполнителя НечетМ – это последовательность команд.
Сколько существует таких программ, которые число 1 преобразуют в число 25, причём траектория вычислений не содержит число 24? Траектория вычислений программы – это последовательность результатов выполнения всех команд программы. Например, для программы 121 при исходном числе 7 траектория будет состоять из чисел 8, 17, 18 [2].
3. Исполнитель Калькулятор преобразует число на экране. У исполнителя есть две команды, которым присвоены номера:
1. Прибавить 1
2. Умножить на 2.
Программа для исполнителя Калькулятор – это последовательность команд. Сколько существует программ, для которых при исходном числе 1 результатом является число 21, при этом траектория вычислений содержит число 10 и не содержит число 17? [2]
4. У исполнителя Удвоитель-Утроитель три команды, которым присвоены номера:
1. прибавь 1
2. умножь на 2
3. умножь на 3.
Первая из них увеличивает на 1 число на экране, вторая увеличивает это число в 2 раза, третья - в 3 раза.
Программа для Удвоителя-Утроителя – это последовательность команд. Сколько существует программ, которые число 1 преобразуют в число 13 [2]?
5. У исполнителя Множик есть две команды:
1. умножь на 8,
2. подели на 2.
Первая из них увеличивает число на экране в 8 раз, вторая – уменьшает его в 2 раза.
Программа для Множика – это последовательность команд. Сколько различных чисел можно получить из числа 512 с помощью программы, которая содержит ровно 8 команд? [2]
Таким образом, задачи по теме «Динамическое программирование» можно разделить на несколько типов: «количество программ с обязательным этапом», «поиск количества программ по заданному числу», «поиск количества чисел по заданному числу команд», для каждого из которых есть свой алгоритм действий. Подробно разобрав каждый тип задания с учеником, отработав каждый алгоритм решения, можно добиться того, что количество ошибок в решении 22 задания ЕГЭ по информатике значительно сократиться.
Список литературы
- Босова, Л. Л. Электронное приложение к учебнику «Информатика» для 10 класса [Электронный ресурс]. / Л. Л. Босова и др. // УМК 10-11 кл. Бином. Лаборатория знаний. – Режим доступа : http://shkola8kuznetsck.narod.ru/uchebniki/informatika10Bosova.pdf
- Решу ЕГЭ. Образовательный портал для подготовки к экзаменам: информатика [Электронный ресурс]. // Информатика: каталог заданий. – Режим доступа : https://inf-ege.sdamgia.ru/?redir=1
- Поляков, К. Ю. Информатика. 10 класс. Углубленный уровень: учебник в 2 ч. Ч. 1 [Текст]. / К. Ю. Поляков, Е. А. Еремин. – М. : БИНОМ, Лаборатория знаний, 2013. – 344 с.