Электронный научный журнал

Информационно-коммуникационные технологии
в педагогическом образовании

РЕШЕНИЕ ЗАДАЧ ПО ПРОГРАММИРОВАНИЮ ПО ТЕМЕ «ЗАДАЧИ НА ПЕРЕБОР»

Раздел: Профессиональное образование и технологическое обучение в РФ и за рубежом

Журнал: Материалы XIV Международной научно-практической конференции

30 декабря 2019 г.

Авторы: Валов Иван Александрович

УДК 004.021

И. А. Валов

I. A. Valov

Валов Иван Александрович, студент 4 курса, ФИМЭ, НФИ КемГУ, г. Новокузнецк, Россия.
Научный руководитель: Можаров Максим Сергеевич, канд. пед. наук, профессор, зав. кафедры ИОТД ФГБОУ ВО НФИ КемГУ, г. Новокузнецк, Россия.

Valov Ivan Alexandrovich, 4th year student, FIME, NFI KemSU, Novokuznetsk, Russia.
Scientific adviser: Mozharov Maksim Sergeevich, Candidate of Pedagogical Sciences, Professor, Head of the Department of Engineering and Technology, FSBEI HE NFI KemSU, Novokuznetsk, Russia.

 

РЕШЕНИЕ ЗАДАЧ ПО ПРОГРАММИРОВАНИЮ ПО ТЕМЕ «ЗАДАЧИ НА ПЕРЕБОР»

SOLUTION OF PROGRAMMING PROBLEMS ON THE TOPIC «PROBLEM TASKS»

 

Аннотация. В статье приведен подробный разбор задач по программированию повышенной сложности по теме «Задачи на перебор», которые используются на олимпиадах по информатике среди школьников. Целью статьи является подготовить школьников и студентов к решению задач, представленных на олимпиадах по информатике.

Abstract. The article provides a detailed analysis of programming problems of increased complexity on the topic «Tasks for busting», which are used at computer science competitions among students. The aim of the article is to prepare schoolchildren and students to solve the problems presented at the informatics olympiads.

Ключевые слова: программирование, задачи, задачи на перебор, олимпиадные задачи, задачи повышенной сложности, Pascal.

Keywords: programming, tasks, enumeration problems, olympiad problems, problems of increased complexity, Pascal.

 

Решение задач методом перебора относится к классу методов поиска решения исчерпыванием всевозможных вариантов [1].

Схема перебора всегда одинакова:

  1. Необходимо установить порядок на элементах, подлежащих перечислению (т.е. определить, какой будет первым, а какой вторым)
  2. Научится переходить от произвольно элемента к непосредственно следующему за ним (т. Е. для заданного элемента х1 стоить такой элемент х2, что х1<х2 и между х1 и х2 нет других элементов) [2].

Решение задачи путем перебора сопровождается использованием циклических алгоритмов. В каждом цикле проверяется, подходит ли этот параметр для условия задачи [3].

Далее будем рассматривать типовые задачи, решаемые на олимпиадах по программированию.

Теория

Пока запишем схему перебора в таком виде:

X:=First;
while X<>Last do Next(X);

где First – первый элемент; Last – последний элемент; Next – процедура получения следующего элемента.

Задача 1

Обозначим: k – номер рейса судна, i – номер очередного груза, s – масса груза на судне в k-том рейсе.

Решать задачу будем так: если на судно в k-том рейсе можно поместить ещё один груз, то мы грузим его и берём следующий, если груз не может быть размещен, то перевозим его следующим рейсом (увеличиваем k).

Основная часть соответствующей программы будет иметь вид:

k:=1;

i:=1;

s:=0;

repeat if s+m[i]<=50 then

   begin

        s:=s+m[i];

        i:=i+1;

    end

            else begin k:=k+1;

     s:=0;

     end;

until i>15;

writeln('Всего потребовалось', k,' рейсов');

Задача 2

Пусть двумя числами (H и V) задано положение коня на шахматной доске. Найдите координаты всех клеток, куда конь может пойти следующим ходом (других фигур на доске нет).

В данном примере, вариантами решения являются координаты клеток, то есть каждый вариант это не одно число, а два. Необходимо придумать способ вычисления варианта (в данном случае номеров горизонтали и вертикали) по его номеру.

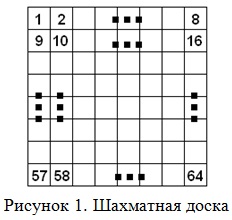
Всего клеток 64. Пронумеруем клетки, как показано на рисунке 1. Теперь, если мы будем перебирать в цикле номера клеток N, необходимо уметь по этим номерам определять номер горизонтали X и вертикали Y. Нетрудно видеть, что номер горизонтали определяется тем сколько раз по 8 клеток надо взять, пока мы не доберемся до числа N:

X := (N - 1) div 8 + 1;

(N - 1) потому что важно сколько горизонталей заполняют клетки, лежащие до N-й, а их как раз N - 1.

Остаток после удаления целого числа раз по 8 клеток позволит вычислить номер вертикали:

Y := (N - 1) mod 8 + 1;

Теперь, когда мы умеем перебирать варианты, необходимо записать условие того, что данный вариант является решением задачи. Известно, что конь ходит буквой Г, смещаясь на две клетки в одном направлении и на одну в другом. Например, на рисунке 2 показан ход, когда перемещение коня состоит из сдвига на две клетки по вертикали и на одну по горизонтали.

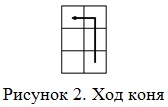
Пусть проверяется клетка с координатами (x, y). Тогда условие сдвига по горизонтали на 2 будет выглядеть так: abs(X-H)= 2.

Взятие модуля необходимо, чтобы учесть возможность сдвига как вправо, так и влево. Аналогично условие сдвига на одну клетку, например, по вертикали: abs(Y-V).

Полное условие возможности пойти на клетку конем будет выглядеть как: ((abs(X-H) = 2)and(abs(Y-V) = 1)) or ((abs(Y-V) = 2)and(abs(X-H) = 1))

То есть либо сначала по горизонтали на две клетки, а потом на одну по вертикали либо на две по вертикали, потом на одну по горизонтали.

Теперь, когда ясно как перебирать клетки и как проверять возможность хода, можно написать требуемую программу:

  Readln (H, V);   {запрашиваем расположение коня}

  for n:=1 to 64 do //цикл

  begin

    X := n div 8 + 1;

    Y := n mod 8;

    if ((abs(X-H) = 2) and(abs(Y-V) = 1)) or ((abs(Y-V) = 2) and(abs(X-H) = 1))

then

      writeln (X, Y); //вывод с новой строки

  end;

В случае, когда как в приведенном примере, каждый вариант задается не одним числом, а несколькими, удобно для перебора использовать вложенные циклы. В данном случае номера вертикали и горизонтали являются целым числами от 1 до 8, поэтому для перебора их значений можно использовать счетчики циклов:

readln(H, V);

  for X:=1 to 8 do //цикл

    for Y:=1 to 8 do //цикл

      if ((abs(X-H) = 2)and(abs(Y-V) = 1)) or ((abs(Y-V) = 2)and(abs(X-H) = 1)) then

        writeln(X, Y); //вывод с новой строки

Задача 3

Составить программу-генератор пифагоровых троек. Пифагоровой тройкой называют такие целые числа a, b и c, которые удовлетворяют условию a²+b²=c². Известно, что существует прямоугольный треугольник с такими длинами сторон. Найдем все пифагоровы тройки для c < 5.

Тройное вложение циклов позволит перебрать все возможные комбинации значений трех чисел a, b и c и вывести те из них, которые удовлетворяют заданному равенству.

MaxC:=25;   { используем параметризацию}

  MaxAB:=trunc(sqrt(MaxC));

  for a:=1 to MaxAB do //цикл

    for b:=1 to MaxAB do //цикл

      for c:=1 to MaxC do //цикл

        if a*a+b*b = c*c then

        begin

          write(a, '   ', b, '   ', c);

          writeln;

        end;

Как всегда, при решении задачи методом перебора, следует задуматься, можем ли мы сократить число перебираемых вариантов. Оказывается, можно ограничиться только перебором a и b, а c вычислять по теореме Пифагора Описание: c=sqrt{a^2+b^2} Вычисленное таким образом c может оказаться нецелым, поэтому условие задачи для него проверять все равно необходимо.

MaxC:=25;  {Используем параметризацию}

  MaxAB:=trunc(sqrt(MaxC));

  for a:=1 to MaxAB do

  begin

    for b:=1 to MaxAB do

    begin

      c:=round(sqrt(a*a+b*b));

      if a*a+b*b = c*c then

      begin

        write(a, '   ', b, '   ', c);

        writeln;

      end;

    end;

  end;

Задачи для самостоятельного решения:

  1. Для заданного числа x распечатать числовую последовательность: sin(x), sin(sin(x)), sin(sin(sin(x))), …
    Вычисления прекратить, когда очередной элемент последовательности станет по модулю меньше, чем .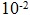
  2. Для любого целого числа N > 7 найти все такие пары целых чисел x и y, что 3x + 5y = N.
  3. Подсчитать количество сочетаний из N элементов по M (N>M). Для подсчета количества сочетаний используется формула:
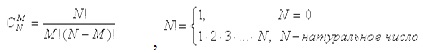
    Описание: http://dist-olimpiada.krasnogorka.edusite.ru/images/frml1.gif
  4. Построить алгоритм, выдающий без повторений все перестановки N чисел.
  5. Сгенерировать все k-элементные подмножества множества A из N чисел, A = {1, 2, ..., N}.
    Пример: N = 3, k = 2, подмножества {1, 2}, {1, 3}, {2, 3}.
  6. Показать, что любую сумму, большую 7 копеек, можно выплатить, используя только 3-х и 5-ти копеечные монеты. (То есть, для любого целого N > 7 найти такие целые числа x и y, что 3x + 5y = N).
  7. Построить все слова длины n>0 в алфавите скобок "(" и ")", представляющие правильные скобочные записи.
  8. Подсчитайте количество одно-, двух-, трёх- и четырехпалубных кораблей, расположенных на поле для игры «Морской бой». Корабли не могут быть изогнутыми и друг с другом не соприкасаются. Поле для игры задается в виде таблицы 10x10, каждый элемент которой равен либо 0, если клетка свободна, либо 1, если занята.

Заключение

В данной статье мы привели типовые решения задач повышенной сложности по теме «Задачи на перебор». Решение таких задач помогает школьникам и студентам при решении олимпиадных задач, и закрепляет знания. А для учителя по информатике данная статья является методическим пособием, с помощью которого учитель может дать знания учащимся.

Список литературы

  1. Можаров, М. С. Введение в структурное программирование: Учебное пособие [Текст]. / М. С. Можаров, Г. Н. Бойченко. – Новокузнецк : Изд-во КузГПА, 2014. – 203 с.
  2. Задачи на перебор вариантов [Электронный ресурс]. – Режим доступа : http://www.tvd-home.ru/prog/6_1
  3. Задачи на перебор вариантов [Электронный ресурс]. – Режим доступа : http://dist-olimpiada.krasnogorka.edusite.ru/p19aa1.html
PDF