ОБУЧЕНИЕ РЕШЕНИЮ КОМБИНАТОРНЫХ ЗАДАЧ УЧАЩИХСЯ ОСНОВНОЙ ШКОЛЫ
Раздел: Материалы I Всероссийской очно-заочной практической конференции "Математика, физика, информатика:проблемы и перспективы современного образования" (Новокузнецк, февраль 2016)
Журнал: Проблемы и перспективы современного математического образования
6 июня 2016 г.
Авторы: Долматова Татьяна Альбертовна , Зайцева Л. И.
Т. А. Долматова, Л. И. Зайцева
ОБУЧЕНИЕ РЕШЕНИЮ КОМБИНАТОРНЫХ ЗАДАЧ УЧАЩИХСЯ ОСНОВНОЙ ШКОЛЫ
В различных жизненных ситуациях человеку приходится иметь дело с задачами, в которых необходимо подсчитать число всех возможных вариантов расположения предметов или число способов осуществления некоторого действия. Такие задачи приходится решать при организации автоматической телефонной связи, при организации работы морских портов, при определении наиболее выгодных коммуникаций внутри населенных пунктов, при составлении расписаний занятий в учебных заведениях, при распределении различных видов трудовой деятельности между рабочими, при составлении расписаний движения различного вида транспорта и так далее. Выбираемые пути или варианты складываются в разнообразные комбинации.
Целый раздел математики, называемый комбинаторикой, занят поиском ответов на вопросы: сколько всего имеется различных комбинаций и каких именно в том или в другом случае.
Комбинаторика – область математики, изучающая количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, принадлежащих конечному множеству. В математике довольно часто приходится иметь дело с различного рода множествами, подмножествами: устанавливать связь между элементами каждого, определять число множеств или их подмножеств, обладающих определенными свойствами.
Общими задачами комбинаторики являются следующие:
1. Найти конфигурацию элементов, обладающую ранее заданным свойством.
2. Доказать существование или отсутствие конфигурации с заданными свойствами.
3. Найти общее число конфигураций с заданными свойствами.
4. Описать все способы решения данной комбинаторной задачи, дать алгоритм перечисления.
5. Из всех решений данной комбинаторной задачи выбрать самое оптимальное по тем или иным параметрам [1].
Современный школьник так же, как и взрослый человек, должен развивать в себе способность выбирать один наилучший из нескольких вариантов решений, уметь оценивать свои шансы на успех, оценивать степень риска в игровых и повседневных жизненных ситуациях. Изучение элементов комбинаторики и вероятности имеет важное значение для развития логического мышления и поэтому, чем раньше школьники начнут изучать данные вопросы, тем проще будет происходить перестройка их психической деятельности.
Исследования психологов показывают, что человек по своей природе не достаточно приспособлен к вероятностно-статистической информации. Работы психологов утверждают, что наиболее благоприятен для формирования вероятностных представлений возраст 10-13 лет. Экспериментальная работа в 5-х и 6-х классах по пропедевтике вероятностных представлений, проведению экспериментов со случайными исходами и обсуждению на качественном уровне их результатов показало, что этот не закрепленный формальными «обязательными результатами» период дает хорошее развитие вероятностной интуиции и статистических представлений детей.
Кроме того, согласно многочисленным проведенным исследованиям учащихся 5 – 9-х классах средней школы, у них происходит падение интереса к математике и к процессу обучения. На уроках математики в основной школе в пятых-девятых классах, проводимых в традиционной форме, у учеников возникают проблемы с изучаемыми объектами, отсутствуют необходимые взаимосвязи между изучаемыми объектами и окружающим миром. Введение элементов комбинаторики, теории вероятности способствует возвращению интереса к предмету «математика», как к таковому.
Введение элементов комбинаторики позволяет развивать комбинаторный стиль мышления, который в дальнейшей жизни позволит школьнику определиться как в профессиональной деятельности, так и в общекультурной жизни. Владение комбинаторными знаниями позволяет учащимся анализировать факты, оценивать шансы, прогнозировать развитие ситуации, принимать решения в нестандартных ситуациях. Поэтому введение элементов комбинаторики в школьное математическое образование является важным решением.
На изучение элементов комбинаторики в курсе математики основной школы выделяется в соответствии с примерной программой 12 – 14 часов, что является недостаточным для прочного усвоения знаний, так как в настоящее время задания по разделу «Элементы комбинаторики» входят в состав основного государственного экзамена по математике в модуле «Реальная математика».
Результаты проведения ОГЭ показывают, что треть всех учащихся, сдававших экзамен, не справляются с заданиями по теории вероятности, задачами по комбинаторике. Комбинаторные знания используются в сложных случаях вычисления числа исходов.
Для успешной сдачи основного государственного экзамена учащиеся должны освоить методы решения перечислительных задач; задач, при решении которых применяются правило суммы и правило умножения, задач с непосредственным применением формул для нахождения числа перестановок, размещений и сочетаний, как с повторением элементов, так и без повторения.
Задачи на перечисление элементов решаются с помощью таблиц или построением дерева (графа). При больших значениях элементов множества перебор вариантов - работа трудоемкая, поэтому для решения таких задач применяют формулы для подсчета числа возможных комбинаций. Эти формулы получаются с помощью правил суммы и умножения.
Ученик не просто должен знать эти правила, но и хорошо ориентироваться, когда и какое из этих правил необходимо применить. Напомним эти правила.
Правило суммы (сложения). Если некоторый объект А можно выбрать m способами, а другой объект B можно выбрать n способами, то выбор «либо А, либо В» можно осуществить m+n способами. Ключевыми словами являются: «либо А, либо В», тогда число способов находим с помощью правила сложения.
Пример. Из множества чисел 1, 2, 7, 9, 6 определить число способов выбора четной или нечетной цифры.
Решение. Четную цифру можно выбрать двумя способами (числа 2, 6), нечетную цифру - тремя способами (числа 1, 7, 9). Тогда выбор четной либо нечетной цифры находим 2+3=5 способами.
Правило умножения. Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать n способами, то выбор пары (А и В) в указанном порядке можно осуществить m × n способами. Ключевыми словами являются «А и В», применяем правило умножения.
Пример. Сколько трехзначных чисел можно составить из цифр 2, 7, 5, 9, используя в записи числа каждую цифру не более одного раза?
Решение. Первую цифру можно выбрать четырьмя способами, так как цифр четыре, вторую цифру можно выбрать тремя способами, так как одна из цифр уже выбрана, третью цифру выбираем двумя способами, так как две цифры уже выбраны. Количество способов составить число можно посчитать следующим образом: 4×3×2 =24 способа.
Многие задачи решаются, используя готовые формулы и определения понятий. Здесь важно определить, о каком точно понятии идет речь (перестановка, сочетание, размещение), а также с повторением эта комбинация или нет. Приведем примеры некоторых видов задач, встречающихся в сборниках, предназначенных для подготовки к ОГЭ.
Задача 1. Найдите вероятность того, что в результате случайной расстановки букв а, б, е, и, к, л, п, р, с, у получится слово «республика» [2].
Решение. Пусть буквы а, б, е, и, к, л, п, р, с, у нужно расположить в один ряд. Сколькими способами это можно сделать. Если не учитывать порядок расположения букв, их можно расположить одним способом, например так, как они записаны: а, б, е, и, к, л, п, р, с, у. Если порядок букв важен, то число способов из расположения можно представить в виде дерева различных вариантов.
Первую букву расположим на одном из десяти мест. Вторую – на любом из девяти оставшихся. Получим 90 вариантов. Третью букву расположим на одном из восьми оставшихся. Получим 720 возможных вариантов. Четвертую букву расположим на одном из семи мест. Получим 5040 вариантов. Пятую букву расположим на одном из шести мест. Получим 30240 возможных вариантов. Шестую букву расположим на одном из пяти мест. Получим 151200 вариантов. Седьмую букву расположим на одном из четырех мест. Получим 604800 возможных вариантов. Восьмую букву расположим на одном из трех мест. Получим 1814400 вариантов. Девятую букву расположим на одном из двух мест. Получим 3628800 возможных вариантов. Последнюю букву расположим на оставшееся место, так как выбора больше нет. То есть существует 3628800 вариантов расположения десяти букв.
Если обобщить задачу на случай перестановок n различных элементов по n местам, получим Pn различных вариантов, используя формулу Pn = n!, т.е. эту задачу можно решить, используя формулу перестановок без повторений: Pn = 10! = 10×9×8×7×6×5×4×3×2×1 = 3628800 равновозможных вариантов расположения.
Благоприятных исходов один, то есть из букв а, б, е, и, к, л, п, р, с, у можно составить только одно слово республика. На основании классического определения вероятности 
получим искомую вероятность 
.
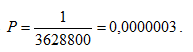Задача 2. Художник случайным образом рисует трехцветный флаг с горизонтальными цветными линиями одной ширины, при этом использует 8 цветов: красный, синий, голубой, темно-зеленый, темно-синий, салатовый, фиолетовый, розовый. Найти вероятность того, что получим флаг, составленный из холодных цветов: темно-синий, синий, голубой?
Решение. В нашем примере важны не только сами цвета полос, но их расположение. При этом принято говорить: «порядок важен, и выбираем 3 из 8». В этом случае имеем дело с размещениями из 8 по 3: 
.
Найдем общее количество расцветок флага составит: 
.
Общее число флагов с холодной раскраской: 
.
Все расцветки равновозможны. Используя классическое определение вероятности, найдем 
.
Задача 3. В классе 18 мальчиков и 12 девочек. Для подготовки классной комнаты к занятиям случайным образом выбирают двух дежурных. Найдите вероятность того, что дежурить будут два мальчика.
Решение. Общее число способов выбрать двух дежурных из 30 (общее число девочек и мальчиков в классе) находим по формуле 
. Принято говорить: «порядок не важен, и выбираем k элементов из n» - значит это сочетания.
Таким образом,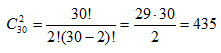 
способами.
Теперь найдем число благоприятных способов выбрать двух мальчиков: 
.
Вероятность найдем, используя классическое определение 
.
Были проанализированы учебники по математике для 5 – 6 классов трех линий: И.И. Зубаревой и А.Г. Мордковича [3, 4]; под редакцией Г.В. Дорофеева и И.Ф. Шарыгина [5,67]; Н.Я. Виленкина, В.И. Жохова, А.С. Чеснокова, С.И. Шварцбурга [7, 8]. Наиболее удачными, по нашему мнению, являются учебники И.И. Зубаревой и А.Г. Мордковича, а также учебники под редакцией Г.В. Дорофеева и И.Ф. Шарыгина, так как учебный материал по элементам комбинаторики сконцентрирован и дан в нескольких параграфах. Задачный материал представлен двумя уровнями: базовым и повышенным. В учебниках Н.Я. Виленкина, В.И. Жохова, А.С.Чеснокова, С.И. Шварцбурга задачи распределены по всему курсу математики в 5-6 классах, что является не всегда удобным, так как от решения одной задачи до другой проходит значительный промежуток времени. Часть пройденного материала не подкрепляется, а значит, может быть потеряна.
В 7 – 9 классах наиболее подробно в курсе алгебры основной школы элементы комбинаторики рассмотрены в учебнике под редакцией С.А. Теляковского. Здесь наиболее полно представлен теоретический материал – рассмотрены основные понятия, формулы, правила, приемы, используемые для решения задач. Кроме самих формул, имеются также и выводы этих формул. Задачного материала достаточно, хотя он не всегда разделен по уровням сложности.
Введение элементов комбинаторики в школьный курс математики позволяет развивать у школьников комбинаторный стиль мышления, который позволит в будущем определиться в жизни. Владение комбинаторными знаниями дает возможность учащимся анализировать факты, оценивать шансы, прогнозировать развитие ситуации, принимать решения в нестандартных ситуациях.
ИНФОРМАЦИОННЫЕ ИСТОЧНИКИ
1. Виленкин Н.Я. Комбинаторика.-М.: Наука, 1969.-328 с.
2. Рязановский А.Р., Мухин Д.Г. Математика. Основной государственный экзамен. Теория вероятностей и элементы статистики.-М.: Экзамен, 2015.-47 с.
3. Зубарева И.И., Мордкович А.Г. Математика. 5 класс: Учебник для учащихся общеобразовательных учреждений.-М.: Мнемозина, 2012.- 270 с.
4. Зубарева И.И., Мордкович А.Г. Математика. 6 класс: Учебник для учащихся общеобразовательных учреждений.-М.: Мнемозина, 2012.-264 с.
5. Математика: Учебник для 5 классов общеобразовательных учреждений / Г.В. Дорофеев и [др.].-М.: Просвещение, 2004.-302 с.
6. Математика. 6 класс: Учебник для общеобразовательных организаций / Г.В. Дорофеев и [др.].-М.: Просвещение, 2014.-287 с.
7. Математика. 5 класс: Учебник для учащихся общеобразовательных учреждений / Н.Я. Виленкин и [др.].-М.: Мнемозина, 2012.-280 с.
8. Математика. 6 класс: Учебник для учащихся общеобразовательных учреждений / Н.Я. Виленкин и [др.].-М.: Мнемозина, 2012.-288 с.