НЕСКОЛЬКО СПОСОБОВ ИЗВЛЕЧЕНИЯ КВАДРАТНЫХ КОРНЕЙ
Раздел: Материалы I Международной очно-заочной научно-практической конференции по математике, физике, информатике, робототехнике, технологии, астрономии учащихся 5-11 классов
Журнал: Научно-исследовательская работа школьников «Мир моих исследований»
28 июня 2017 г.
Авторы: Милюхина Кристина Борисовна
УДК 372.851
К. Б. Милюхина
Муниципальное бюджетное общеобразовательное учреждение Лесоперевалочная СОШ № 2, с. Бельтирское, Аскизский район
НЕСКОЛЬКО СПОСОБОВ ИЗВЛЕЧЕНИЯ КВАДРАТНЫХ КОРНЕЙ
Аннотация. Тема, затронутая в статье, показывает, что изучение квадратных корней, не прихоть математиков, а объективная необходимость: в реальной жизни случаются ситуации, математические модели которых содержат операцию извлечении квадратного корня. Изучив способы извлечения квадратного корня, был создан проект «Несколько способов извлечений квадратных корней».
1-й способ: Способ разложения на простые множители [1]
Для извлечения квадратного корня можно разложить число на простые множители и извлечь квадратный корень из произведения (табл.).
Ученики применяют этот способ успешно и считают единственным. Извлечение корня разложением на множители – трудоёмкая задача, которая не всегда приводит к желаемому результату. Попробуем извлечь квадратный корень из числа 206116. Разложение на простые множители дает произведение 2∙2∙51529. А как быть дальше? В ответе записывают остаток от разложения под знак корня. Чаще мы видим, что корень до конца не извлечь. Поэтому, этот способ лишь частично решает проблему извлечения квадратного корня.
2-й способ: Способ использования таблицы квадратов двузначных чисел [1]
Способ очень прост в применении и даёт мгновенное извлечение квадратного корня из любых целых чисел от 1 до 100 с точностью до десятых.
Найдём значение 
.
Закрываем две последние цифры у всех чисел в таблице квадратов и находим близкие для 73, таких два числа 7225 и 7396 (7396-это много). Рассматриваем число 7225.
Левый столбик таблицы квадратов даёт ответ 8 (целых), а верхняя строка 5 (десятых). Значит 
.
Быстро, просто, доступно на экзамене. Корни большие 100 этим способом извлечь невозможно. Способ удобен для заданий с маленькими корнями и при наличии таблицы.
3-й способ: Формула Древнего Вавилона [4]
Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня из числа Х.
Число Х они представляли в виде суммы 
ближайший к числу Х точный квадрат натурального числа a и пользовались формулой (1).
(1)
Извлечём с помощью этой древней формулы корень квадратный из числа 68:
Результат извлечения корня из 68 с помощью МК равен 8,246211.
Из числа 94:
Результат извлечения корня из 94 с помощью МК равен 9,695359.
Как видим, способ вавилонян даёт хорошее приближение к точному значению корня. Но без знания полных квадратов больших чисел и умения их быстро находить, результат извлечения будет найти затруднительно.
Этот способ являются самым простым и доступным для учащихся школ.
4-й способ: С помощью уравнения [2]
Существует удобный способ нахождения квадратного корня с помощью решения уравнения. В чем его суть рассмотрим на примере и попробуем вычислить значение корня из числа 37.Сначала определим границы искомого корня в целых числах. Легко догадаться, что это числа 
.
Пусть х – это та разница, на которую отличны друг от друга 
,
значит 
. Возведем в квадрат обе части полученного уравнения 
и раскроем скобки при помощи формулы квадрата суммы:
37 = (6 + х)² = 36 + 12х + х².
Так как мы рассчитываем получить результат с точностью до десятых или до сотых, а х² явно достаточно малая дробь, то ей вполне можно пренебречь.
В результате приходим к простому линейному уравнению 37 = 36 + 12х.
Решив его, получаем значение: х = 0,08. Значит 
.
Но и этот способ требует терпения и умения решать уравнения с использованием формул сокращённого умножения.
5-й способ: Канадский метод [5]
Канадский метод был открыт молодыми учёными одного из ведущих университетов Канады в 20 веке. Его точность – не более двух-трёх знаков после запятой. Применяли формулу:
(2)
где X - число, из которого необходимо извлечь квадратный корень, а S - число ближайшего точного квадрата.
Например: извлечь квадратный корень из 86
.
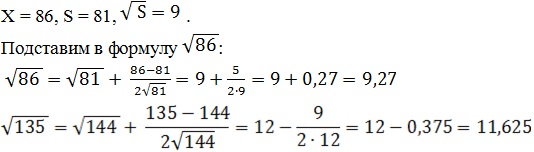Метод несложный и удобный.
6-й способ: Способ вычетов нечётного числа [3]
Способ вычетов нечётного числа заключается в том, чтобы из подкоренного выражения последовательно вычитать нечётные числа 1, 3, 5, 7 и т. д. пока разность не станет равной 0, а затем подсчитать количество вычитаний. Это и будет ответ.
Например: извлечь квадратный корень из 81.
Решение: 81-1=80-3=77-5=72-7=65-9=56-11=45-13=32-15=17-17=0, количество вычитаний = 9, поэтому 
.
Например: извлечь квадратный корень из 225.
Решение: 225-1=224-3=221-5=216-7=209-9=200-11=189-13=176-15=161-17=144-19=125-21=104-23=81-25=56-27=29-29=0,
количество вычитаний = 15, поэтому 
.
Российские учёные называют этот метод арифметическим извлечением квадратного корня, а за глаза «методом черепахи» из-за его медлительности. Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее. В то же время такой способ вполне доступен детям, решающим простейшие математические задачи, требующие извлечения квадратного корня.
7-й способ: Способ отбрасывания полного квадрата (для четырёхзначных чисел) [3].
Этот способ применим только для извлечения квадратного корня из точного квадрата, а алгоритм нахождения зависит от величины подкоренного числа.
1) Извлечение корней до числа 
Например: 
.
Число 1296 представим в виде суммы, выделив из этого числа квадрат 196, затем выделенный квадрат отбрасываем, к числу сотен первого слагаемого (11) прибавляем всегда 25. Получим ответ 36.
Так можно извлекать только квадратные корни до числа 
2) Извлечение корней после числа
Например: 
.
Число 6084 представим в виде суммы 5600 и выделенного квадрата 484. Затем к числу сотен прибавить квадратный корень из 484, равный 22.
Получим ответ 78.
Этот способ очень интересен и оригинален.
Применим только для четырёхзначных чисел точных квадратов.
Список литературы
- Мордкович, А. Г. Алгебра. 8 кл.: В двух частях. Ч.1: Учебник для общеобразовательных учреждений [Текст]. / А. Г. Мордкович. – М.: Мнемозина. – 2012.
- Пичугин, Л. Ф. За страницами учебника алгебры. Книга для учащихся 7–9 классов средней школы [Текст]. / Л. Ф. Пичугин. – М.: Просвещение. – 1990.
- Научно-теоретический и методический журнал «Математика в школе», 1998. – № 6.
- Теорема [Электронный ресурс]. // Википедия: свободная энциклопедия. – Режим доступа : http://ru.wikipedia.ord/wiki/Теорема
- Открытый урок [Электронный ресурс]. // Первое сентября. – Режим доступа : http://festival.1september.ru/
Научный руководитель: учитель математики
Сердюк С. А.