ОДИН ИЗ ПОДХОДОВ К РЕШЕНИЮ УРАВНЕНИЙ С ПАРАМЕТРОМ ГРАФИЧЕСКИМ МЕТОДОМ
Раздел: Материалы II Международной очно-заочной научно-практической конференции «Проблемы и перспективы современного физико-математического, информационного и технологического образования» (Новокузнецк, февраль 2018)
Журнал: Проблемы и перспективы современного физико-математического образования
27 февраля 2018 г.
Авторы: Гридчина Валентина Борисовна
УДК 517.912
В. Б. Гридчина
V. B. Gridchina
Гридчина Валентина Борисовна, кандидат педагогических наук, доцент, НФИ КемГУ, г. Новокузнецк.
Gridchina Valentina Borisovna, candidate of pedagogical Sciences, associate Professor, NFI KemGU, Novokuznetsk.
ОДИН ИЗ ПОДХОДОВ К РЕШЕНИЮ УРАВНЕНИЙ С ПАРАМЕТРОМ ГРАФИЧЕСКИМ МЕТОДОМ
ONE OF THE APPROACHES TO SOLVING EQUATIONS WITH PARAMETERS USING A GRAPHICAL METHOD
Аннотация. В статье рассматриваются примеры использования графика функции f(x)=|x-a|+|x-b| при решении уравнений с параметром. Автор демонстрирует графический метод решения уравнений с модулями и параметрами, которые встречаются в заданиях единого государственного экзамена.
Annotation. In the article examples of using the function graph f(x)=|x-a|+|x-b| for solving equations with a parameter are considered. The author demonstrates a graphical method for solving equations with modules and parameters that occur in tasks of the unified state exam.
Ключевые слова: уравнения с параметром, уравнения с модулем, графический метод решения уравнений.
Keywords: equations with a parameter, equations with a modulus, a graphical method for solving equations.
Задачи с параметрами традиционно считаются одними из самых сложных в школьном курсе математики. Это связано с тем, что не существует единого алгоритма их решения, и каждая задача требует индивидуального нестандартного подхода.
При решении уравнений с параметром, содержащих сумму двух модулей |x-a|+|x-b|, в некоторых случаях целесообразно использовать графический метод решения. Рассмотрим функцию f(x)=|x-a|+|x-b|, где a<b.< p=""> </b.<>
Если раскрыть модули, получим
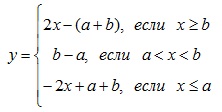
График этой кусочно-заданной функции изображен на рисунке 1.
Рассмотрим несколько примеров, демонстрирующих использование графика функции f(x)=|x-a|+|x-b| при решении уравнений с параметром.
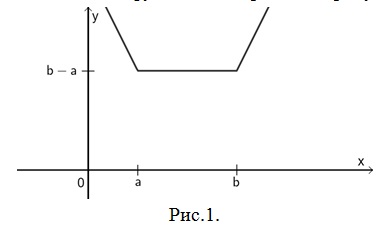
Пример 1. Найти количество корней уравнения |x-1|+|x-3|=2a-3 в зависимости от параметра a.
Решение: Введем функции: y1=|x-1|+|x-3|, y2=2a-3, их графики изобразим в одной системе координат XOY.
Уравнение y2=2a-3 задает семейство прямых, параллельных оси OX, на рисунке 2 они изображены пунктиром. Корни уравнения |x-1|+|x-3|=2a-3 – это абсциссы точек пересечения графиков функций y1 и y2. Из чертежа видно: если 2a-3<2, то корней нет; если 2a-3=2, то уравнение имеет бесконечное множество корней; если 2a-3>2, то уравнение имеет два различных корня.
Ответ: при a<5/2 корней нет; при a=5/2 уравнение имеет бесконечное множество корней; при a>5/2 уравнение имеет два различных корня.
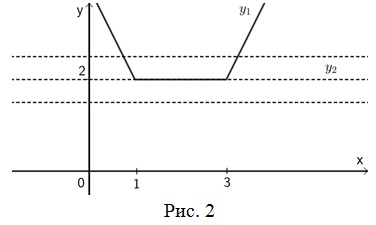
Пример 2. При каких значениях параметра а уравнение |x-2|+|x|=ax+2(a-1) имеет ровно один корень?
Решение: Запишем уравнение в виде: |x-2|+|x|=ax+2(a-1). Введем функции: y1=|x-2|+|x|, y2=ax+2a-2, их графики изображены на рисунке 3.
Уравнение y2=ax+2a-2 задает семейство прямых, проходящих через точку с координатами А(-2;2). На рисунке 3 они изображены пунктиром. Найдем значения параметра, при котором графики функций y1 и y2 пересекаются ровно в одной точке. Уравнение будет иметь один корень, если прямая y2=ax+2a-2 проходит через точку с координатами (2;2). Подставив координаты точки А в уравнение прямой, получим a=1. Из чертежа видно, что уравнение также будет иметь один корень, если угловой коэффициент прямой a<-2 или a≥2.
Ответ: a<-2; a=1; a≥2.
Пример 3. При каких значениях параметра а уравнение 
имеет единственный корень [2]?
Решение: Запишем уравнение в виде 
.
Введем функции: 
, 
, их графики схематично изображены на рисунке 4.
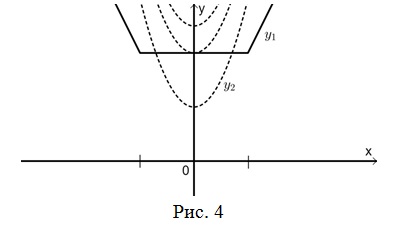
Можно заметить, что функции y1 и y2 четные. Если x0 – корень уравнения, то и -x0 также будет корнем этого уравнения. В нашем случае уравнение будет иметь единственный корень, если этот корень x=0. Подставив x=0 в уравнение, получим: 
или 
, решения которого a=-5, a=-3, a=-1. При a=-3 уравнение имеет три решения x=0 и x=±2. При a=-5 и a=-1 уравнение имеет единственный корень x=0.
Ответ: a=-5, a=-1.
Пример 4. Найти все значения параметра а, при каждом из которых уравнение 
имеет корни, но ни один из них не принадлежит интервалу (4;19) [1].
Решение: Запишем уравнение в виде 
. Так как левая часть уравнения представляет собой сумму двух модулей, то 2a-3≥0, т.е. a≥3/2. Введем функции: 
. Можно заметить, что 
. При a>3/2 их графики изображены на рисунке 5.
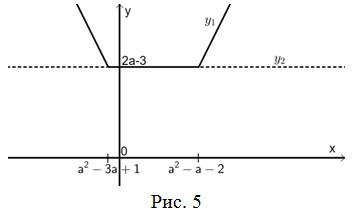
Из чертежа видно, что уравнение имеет бесконечное множество корней. Запишем условия, чтобы ни один из них не принадлежит интервалу (4;19).
или 
. Учитывая, что 
, получим 
.
Отдельно рассмотрим случай a=3/2. Уравнение примет вид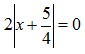 
, решение которого x=-5/4 не принадлежит интервалу (4;19) , а значит a=3/2 удовлетворяет условию задачи.
Ответ: 
.
Пример 5. Найти все значения параметра а, при каждом из которых уравнение 
имеет хотя бы один корень.
Решение: Так как левая часть уравнения представляет собой сумму трех модулей, то a≥0. Преобразуем уравнение к виду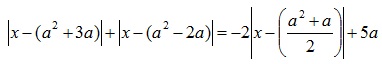
. Введем функции: 
.
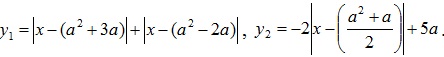При a=0 уравнение примет вид |x|+|x|+|2x|=0, которое имеет решение x=0, а значит, a=0 удовлетворяет условию задачи.
При a>0 графики функций y1 и y2 изображены на рисунке 6. При построении графика функции 
можно заметить, что 
. График функции 
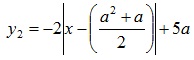можно получить при помощи геометрических преобразований графика функции y=-2|x| (параллельный перенос на 
вдоль оси OX и на 5а вверх).
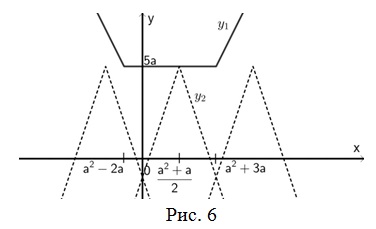
Из чертежа видно, для того чтобы уравнение имело хотя бы один корень, должны выполняться условия: 
. Решая двойное неравенство и учитывая, что a>0, получим 0<a≤5.< p=""> </a≤5.<>
Объединяя с найденным ранее a=0, получим 0≤a≤5.
Ответ: 0≤a≤5.
Рассмотренные задачи можно решать разными методами, но графический метод в данном случае имеет ряд преимуществ: он наглядный и менее трудоемкий, так как не нужно выполнять преобразования с модулями.
Список литературы
- ЕГЭ 2015. Математика. 50 вариантов типовых тестовых заданий [Текст] / И. Р. Высоцкий [и др.] : под ред. И. В. Ященко. – Москва : Экзамен, 2015. – 246 с.
- ЕГЭ Математика. Профильный уровень: типовые экзаменационные варианты: 36 вариантов [Текст] / под ред. И. В. Ященко. – М. : Национальное образование, 2017. – 256 с.