Информационно-коммуникационные технологии
в педагогическом образовании

ОДИН ИЗ СПОСОБОВ ОТБОРА КОРНЕЙ УРАВНЕНИЙ В ЗАДАНИЯХ ЕДИНОГО ГОСУДАРСТВЕННОГО ЭКЗАМЕНА

Раздел: Проблемы и перспективы современного математического образования

Журнал: Материалы III Международной очно-заочной научно-практической конференции. Часть 1

27 марта 2019 г.

Авторы: Осипова Людмила Александровна , Гридчина Валентина Борисовна

УДК 514.11:371.279.6

Л. А. Осипова, В. Б. Гридчина

L. A. Osipova, V. B. Gridchina

Осипова Людмила Александровна, к.п.н., доцент, НФИ КемГУ, г. Новокузнецк.

Гридчина Валентина Борисовна, к.п.н., доцент, НФИ КемГУ, г. Новокузнецк.

Osipova Ludmila Alexandrovna, candidate of pedagogical Sciences, associate Professor, Novokuznetsk Institute (branch) «Kemerovo State University», Novokuznetsk.

Gridchina Valentina Borisovna, candidate of pedagogical Sciences, associate Professor, Novokuznetsk Institute (branch) «Kemerovo State University», Novokuznetsk.

ОДИН ИЗ СПОСОБОВ ОТБОРА КОРНЕЙ УРАВНЕНИЙ В ЗАДАНИЯХ ЕДИНОГО ГОСУДАРСТВЕННОГО ЭКЗАМЕНА

ONE OF THE METHODS OF SELECTING SOLUTIONS OF EQUATIONS IN THE TASKS OF A GENERAL STATE EXAM

Аннотация. В статье анализируются способы отбора корней тригонометрических уравнений. Приводится алгоритм отбора корней уравнений при помощи числовой окружности. Авторы показывают использование данного алгоритма на конкретном примере.

Annotation. The article analyzes the methods of selecting the solutions of trigonometric equations. An algorithm for selecting the solutions of equations using a numerical circle is given. The authors show the use of this algorithm on a specific example.

Ключевые слова: тригонометрические уравнения, способы отбора корней уравнений, числовая окружность.

Keywords: trigonometric equations, methods for selecting solutions of equations, numerical circle.

 

В Единый государственный экзамен по математике входят задания, в которых требуется решить уравнение (тригонометрическое, логарифмическое, показательное или уравнение смешанного типа) и выполнить отбор корней этого уравнения, принадлежащих заданному промежутку. Среди перечисленных уравнений тригонометрические уравнения встречаются чаще других.

В учебно-методической литературе можно встретить четыре основных способа отбора корней тригонометрических уравнений: алгебраический способ (решение двойного неравенства); арифметический способ (перебор по параметру); геометрический способ (с помощью числовой окружности); графический (с помощью графика функции).

В процессе анализа указанных способов отбора корней можно выделить самый оптимальный – отбор корней с помощью числовой окружности. С одной стороны, данный способ является самым наглядным. С другой стороны, его использование позволяет с помощью одной окружности отобрать нужные корни из всех совокупностей решений, а также он удобен в случае, когда ответ содержит не табличное значение аркфункции.

Алгоритм отбора корней с помощью числовой окружности:

1. Построить числовую окружность (схематично).
2. Отметить на окружности промежуток (дуга окружности) в соответствии с условием задачи.
3. Изобразить точками на числовой окружности все получившиеся корни, выделяя из них попавшие в данный промежуток.
4. Назвать эти корни в соответствии с границами промежутка.
5. Записать в ответ полученные корни.

Рассмотрим использование предложенного алгоритма на конкретном примере. Пусть при решении уравнения был получен ответ: . Нужно отобрать корни, принадлежащие промежутку [1].

Решение

1. Строим числовую окружность.
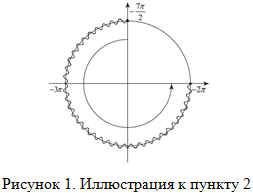
2. Отмечаем на окружности начало промежутка 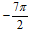(рис. 1), затем движемся по окружности в положительном направлении (против часовой стрелки), пока не доходим до правого конца промежутка -2π, после этого выделяем на окружности заданный промежуток. Для удобства отмечаем точку -3π, так как она находится в нашем промежутке и поможет в дальнейшей записи решения.
   
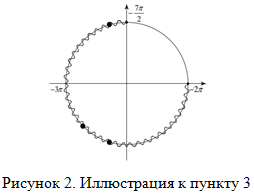
3. Отмечаем точками на окружности (рис. 2) только те корни, полученные при решении уравнения, которые попадают в заданный промежуток. Для удобства сначала не подписываем их.
   
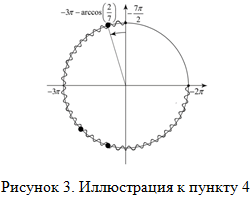
4. В соответствии с рисунком 3, движемся от точки -3π до первой отмеченной точки. При этом замечаем, что нам нужно пройти дугу равную 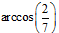, так как движение идет по часовой стрелке, то величину дуги берем со знаком «минус». Значит, первый отобранный корень равен 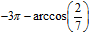. Подписываем его на окружности и выписываем как один из отобранных корней.
   
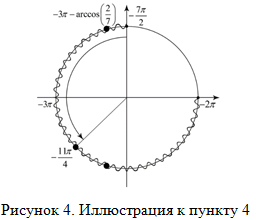
   В соответствии с рисунком 4, во вторую отмеченную точку попадаем, когда проходим после числа -3π дугу равную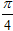 (против часовой стрелки). Следовательно, этот корень равен 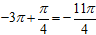. Подписываем его на окружности, и выписываем в список отобранных корней.
   
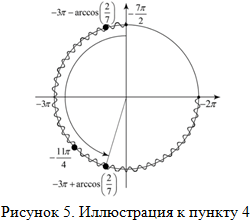
   В соответствии с рисунком 5, в третью точку мы попадаем, когда проходим от точки -3π дугу равную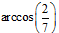 (против часовой стрелки). Соответственно, этот корень равен 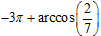. Подписываем и заносим в список.
   
5. Так как других корней на заданном промежутке нет, записываем ответ: .

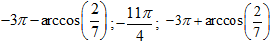Для усвоения предложенного алгоритма необходимо отработать отдельно его шаги, рассматривая при этом всевозможные частные случаи (ответ содержит не табличное значение аркфункции, длина промежутка превосходит  и т.д.).

Список литературы

1. Образовательный портал для подготовки к ЕГЭ [Электронный ресурс]. – Режим доступа : http://reshuege.ru/test?theme=59 (дата обращения : 15.01.2019).